Vlastnosti kombinačních čísel ilustruje následující schéma, které se nazývá Pascalův trojúhelník:

Pokud si čísla ve schématu vyčíslíme, dostaneme Pascalův trojúhelník tvaru:
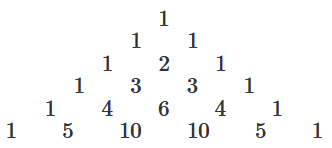
Pascalův trojúhelník má využití u tzv. binomické věty, která říká:
(a+b)^{n} = \sum_{k=0}^{n} {n \choose k} a^{n-k}b^{k}, \ a, b \in \R; n \in \N
Tuto větu lze vysvětlit také následujícím způsobem:
Mějme vzorce (a+b)^3=a^3+3a^2b+3ab^2+b^3 a (a-b)^3=a^3-3a^2b+3ab^2-b^3. Zmiňované vzorce není nutné si pamatovat, jelikož je lze rychle odvodit podle následujícího schématu.
Načrtneme si trojúhelník, jehož dvě strany jsou složeny pouze z jedniček. Vnitřek trojúhelníku je složen s čísel, které jsou součtem dvou čísel nad. Tento trojúhelník se nazývá Pascalův trojúhelník.
Začněme nejprve vzorcem (a+b)^3=a^3+3a^2b+3ab^2+b^3. Závoraka je umocňena na třetí, proto vezmeme třetí řádek, ve kterém se nachází číselná kombinace 1-3-3-1. Protože je v závorce součet, výsledný rozložený výraz bude obsahovat samá +.
Další věcí, kterou je nutno si uvědomit, jsou exponenty v rozloženém výrazu u proměnných a, b. Závorka je umocněna na třetí, pak tedy začneme a^3b^0. Protože cokoliv umocněno na nultou je jedna, pak tedy a^3.
U dalšího čísla postupně snižujeme exponent u proměnné a a naopak zvyšujeme u proměnné b. Podívejme se na třetí řádek trojúhelníku a vidíme číselnou kombinaci 1-3-3-1. Této kombinaci budou odpovídat členy a^3b^0 - a^2b^1 - a^1b^2 - a^0b^3. Pak tedy:
(a+b)^3=1a^3b^0 + 3a^2b^1 + 3a^1b^2 + 1a^0b^3=\\=a^3+3a^2b+3ab^2+b^3
Podívějme se, pokud bychom měli výraz (a+b)^5. Podíváme se do Pascalova trojúhelníku a vidíme číselnou kombinaci 1-5-10-10-5-1. V závorce je +, pak tedy i ve výsledném výrazu bude všude +. Exponenty u proměnné a postupně snižujeme z čísla 5. U proměnné b naopak jdeme z 0 do čísla 5
(a+b)^5=1a^5b^0+5a^4b^1+10a^3b^2+10a^2b^3+5a^1b^4+1a^0b^5=\\=a^5+5a^4b+10a^3b^2+10a^2b^3+5ab^4+b^5
Jak by to bylo, pokud bychom měli vzorec s rozdílem, tedy
(a-b)^3=a^3-3a^2b+3ab^2-b^3
Postup je úplně stejný jako v předchozích příkladech, kdy se v závorce objevil součet. Jediným rozdílem je pouze změna znamének ve finálním výrazu. Tato změna je provedena tak, že každé druhé plus v předchozích příkladech nahradíme mínusem, tedy namísto kombinace + + + + budeme mít kombinaci + - + - . Porovnejme:
(a+b)^3=a^3+3a^2b+3ab^2+b^3
(a-b)^3=a^3-3a^2b+3ab^2-b^3
(a+b)^5=a^5+5a^4b+10a^3b^2+10a^2b^3+5ab^4+b^5
(a-b)^5=a^5-5a^4b+10a^3b^2-10a^2b^3+5ab^4-b^5
!!!Pozor, tento postup neplatí pro vzorce a^3+b^3, a^3-b^3, a^4+b^4, a^4-b^4, atd. V tomto případě nejsme schopni nalézt podobné univerzální řešení a je nutné využít tabulky.