Obor hodnot funkce
Obor hodnot funkce označovaný H_f nebo H(f) představuje všechny hodnoty y (výstupy), kterých funkce nabývá.
Je to množina všech y (výstupů či výsledků), která jsou funkcí přeřazená všem hodnotám x (vstupům) z definičního oboru funkce.
Takové hodnoty y (výstupy) získáme pokud dosazením za x (vstupy) všechny smysluplné hodnoty.
Z grafu snadněji poznáme definiční obor funkce i obor hodnot funkce. Definiční obor D_f hledáme na ose x. Na ose x čteme zleva doprava.
Obor hodnot H_f hledáme na ose y. Na ose y čteme zespoda nahoru.
Příklad: Funkce je dána následujícím grafem. Určete definiční obor funkce a obor hodnot funkce.
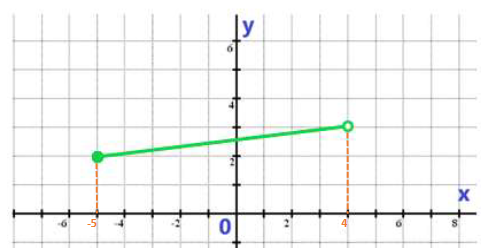
Z kapitoly intervalů již víme, že plné kolečko znamená, že s krajním bodem počítáme, prázdné kolečko znamená, že s krajním bodem nepočítáme.
Řešení: D_f = \langle -5 ; 4 ), H_f = \langle 2 ; 3)
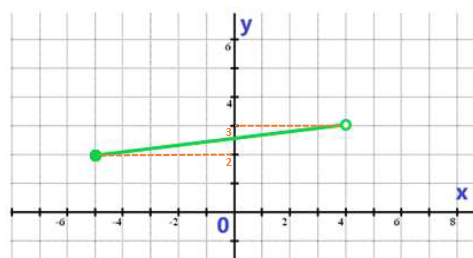
Příklad:
Řešení: D_f = \langle -2 ; 1 \rangle , H_f = \langle -6 ; 4 \rangle
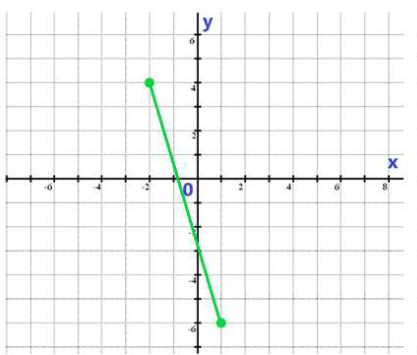
Příklad:

Řešení: D_f = ( -6 ; 6 ) , H_f = ( 1 ; 6 )
Příklad:
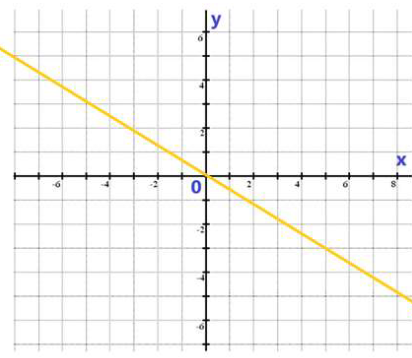
Řešení: D_f = \R , H_f = \R
Příklad:
Ne vždy musí být funce spojitá (spojitá = nepřerušovaná). V následujícím příkladě je funkce, jejíž definiční obor a obor hodnot je dán sjednocením intervalů.
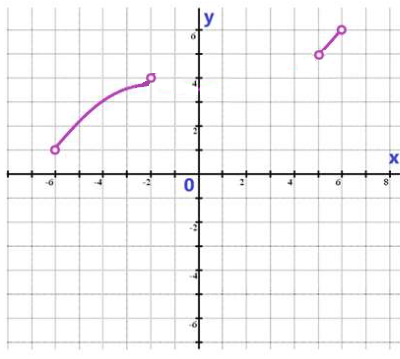
Řešení: D_f = (-6;-2) \cup (5;6) , H_f = (1;4) \cup (5;6)
Výpočet oboru hodnot
Výpočet oboru hodnot bez znalosti grafu funkce se vypočítá několika metodami, které však nejsou univerzální. Může se využít metoda dosazení koeficientu či aplikací inverzní funkce. Všechny tyto metody budou přiblíženy při probírání konkrétních funkcí (kvadratická, exponenciální, ...).