Definiční obor
Definiční obor funkce jsou hodnoty (nejčastěji interval), které můžeme bez omezení dosadit za proměnnou ve výrazu funkce, přičemž po dosazení bude mít výraz smysl.
Příklad č. 1: Mějme graf funkce, u které máme určit definiční obor.
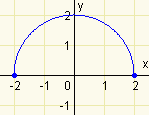
Z grafu je vidět, že funkce f je definována jen pro hodnoty x \in \langle -2;2 \rangle . Definiční obor funkce f pak zapíšeme
D(f) = \langle -2;2 \rangle
nebo
D_f = \langle -2;2 \rangle
Příklad č. 2: Mějme předpis funkce g(x) = \frac{1}{x} a určete její definiční obor.
Vidíme, že nulou dělit nelze, proto definiční obor zapíšeme
D(g) = (- \infty;0) \cup (0;\infty)
nebo
D(g) = \R - \{ 0 \}
nebo
D_g = \R - \{ 0 \}
nebo
D_g = (- \infty;0) \cup (0;\infty)
nebo
D(f) = \R \backslash (2 ;\frac{5}{2} \rangle
nebo
D_f = \R \backslash (2 ;\frac{5}{2} \rangle
Nejčastější typové příklady na určování definičního oboru funkce:
- Neumíme dělit nulou
f: y=\frac{1}{x-3}
Vidíme, že ve jmenovateli nesmí být po dosazení za proměnnou nula, platí tedy:
x-3 \neq 0 \Rightarrow x \neq 3. Definičním oborem funkce je tak množina:
D_f = \R - \{ 3 \} \\ D(f) = \R - \{ 3 \} \\ D(f) = \R \backslash \{ 3 \}
- Odmocnina (sudá)
V případě sudé odmocniny, tedy druhé, čtvrté, šesté, atd. musí být ve výrazu pod odmocninou nezáporné číslo. Definičním oborem funkce g:y=\sqrt{x-3} je tak množina, pro kterou platí:
x-3 \ge 0 \Rightarrow x \ge 3
Definičním oborem funkce je tak
D_g = \langle 3; \infty ) \\ D(g) = \langle 3; \infty )
- Odmocnina (lichá)
V případě liché odmocniny, tedy třetí, pátá, sedmá, atd. může být ve výrazu pod odmocninou libovolné číslo (kladné, záporné, nula). Definičním oborem funkce z:y= \sqrt[3]{x-3} je tak množina:
D_z = \R \\ D(z) = \R
- Kombinace jmenovatele a odmocniny
Mějme funkci f: y= \sqrt{\frac{x-2}{2x-5}} a určeme definiční obor funkce. Při určování definičního oboru funkce je důležité v tomto typu příkladu nezapomenout na žádnou operaci (odmocnina, dělení nulou, ...)
V případě, že mám celý zlomek pod sudou odmocninou, je nutné si také uvědomit, kdy bude zlomek nezáporný. Nastane to v případě, kdy bude čitatel kladný nebo nula a zároveň jmenovatel kladný nebo kdy bude čitatel záporný nebo nula a zároveň jmenovatel záporný.
Pro možnost nezáporného čitatele a kladného jmenovatele dostáváme:
(x-2 \ge 0) \wedge (2x-5 > 0) \\ (x \ge 2) \wedge (x > \frac{5}{2})
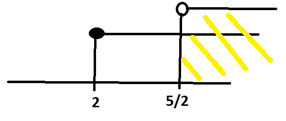
Pro moznost záporného nebo nulového čitatele a záporného jmenovatele dostáváme:
(x-2 \le 0) \wedge (2x-5 < 0) \\ (x \le 2) \wedge (x < \frac{5}{2})
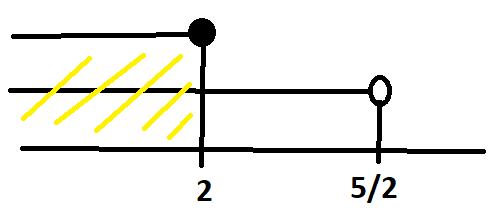
Průnikem těchto dvou intervalů (žlutě vyznačené) dostáváme výsledný definiční obor:
D(f) = (\infty;2 \rangle \cup ( \frac{5}{2};\infty)
nebo
D_f = (\infty;2 \rangle \cup ( \frac{5}{2};\infty)
nebo
D(f) = \R - (2 ;\frac{5}{2} \rangle
nebo
D_f = \R - (2 ;\frac{5}{2} \rangle
nebo
D(f) = \R \backslash (2 ;\frac{5}{2} \rangle
nebo
D_f = \R \backslash (2 ;\frac{5}{2} \rangle
Co je a co není funkce?
Aby byla funkce funkcí, musí platit jedna důležitá vlastnost. Musí platit, že pro každý jeden konkrétní vstup musí existovat právě jeden výstup. Jinak řečeno, pokud dosadím proměnnou ve výrazu libovolné číslo z definičního oboru, musím vždy dostat právě jednu hodnotu.
Matematicky zaspáno: \forall x \in D_f:\ \exists! y \in \R
Příklad: Mějme y=x+2, pak funkční hodnota v bodě 1 je rovna f(1) = 3. Funkční hodnota v bodě 2 je rovna f(2) = 4. Vidíme, že se jedná o předpis, jelikož pokaždé, kdy dosadíme za proměnnu x libovolné číslo z definičního oboru funkce, dostaneme vždy pouze jeden výstup.
Příklad: Mějme |y|=x+2. Dosadíme hodnotu 0:
f(0) = \pm 2
Vidíme, že pro jeden konkrétní vstup x, tedy hodnotu x=0 jsme dostali dva různé výstupy y= \pm 2. Tedy |y|=x+2 není předpis funkce.
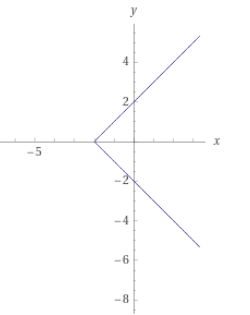
Příklad: Je výraz y^2 + x = 4 funkcí? Opět musí platit, že pro jednu hodnotu x dostáváme právě jednu hodnotu y. Pokud dosadím x = 0, pak dostávám y^2=4. Tato rovnice má dvě různá řešení, a to hodnoty \pm 2.
Můžeme tedy říci, že y^2 + x = 4 není předpis funkce.
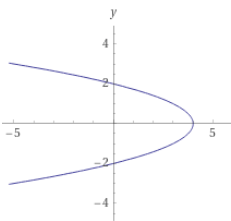
Na následujícím obrázku si můžeme prohlédnout grafickou interpretaci funkce. Vidíme, že funkce a) není funkcí, jelikož pro jedno x dostaneme dvě y. Ostatní grafy už funkcemi jsou.
Graf funkce
Funkci lze studovat pouze pomocí předpisu. Pokud si ji ale vizualizujeme, tak jsme schopni blíže určit mnoho různých vlastností (souměrnost, rostoucí, klesající, ...). Poznáme také názorněji, jak se funkce chová na svém definičním oboru.
Mějme funkci f: y = x+2 . Pouze pro upřesnění, tento výraz je ekvivalentní s jiným zápisem funkce f(x) = x+2.Platí tedy:
f: y = x+2 \Leftrightarrow f(x) = x+2
Postupným dosazováním za hodnotu x dostáváme hodnotu y a uspořádané dvojice [ x ; y ] . Spočteme si konkrétní hodnoty:
f(-1) = -1 + 2 = 1
f(0) = 0 + 2 = 2
f(1) = 1 + 2 = 3
f(2) = 2 + 2 = 4
Získávám tak uspořádané dvojice [-1;1], [0;2], [1;3], [2;4] . Následně body zapíšeme do kartézské soustavy souřadnic a propojíme. Grafem může být přímka, parabola, hyperbola či nespočet jiných křivek. To, jaká křivka bude grafem funkce, lze v mnoha případech odhadnout z předpisu funkce na základě zkušenosti.
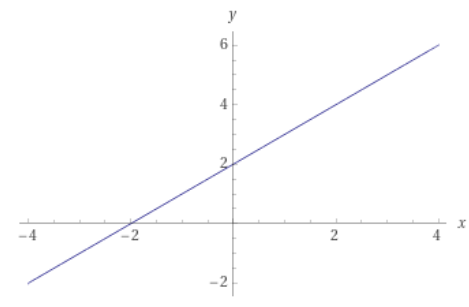
Průsečík funkce s osami
Mějme libovolnou funkci a zjistěme, v jakých bodech má funkce průsečík / průsečíky s osami x a y
(pozn.: s osou y může mít každá funkce maximálně jeden průsečík. V případě, že by měla průsečíky dva, neplatila by základní podmínka pro funkce, a to jest že pro každou hodnotu x můžeme dostat nejvýše jednu hodnotu y.
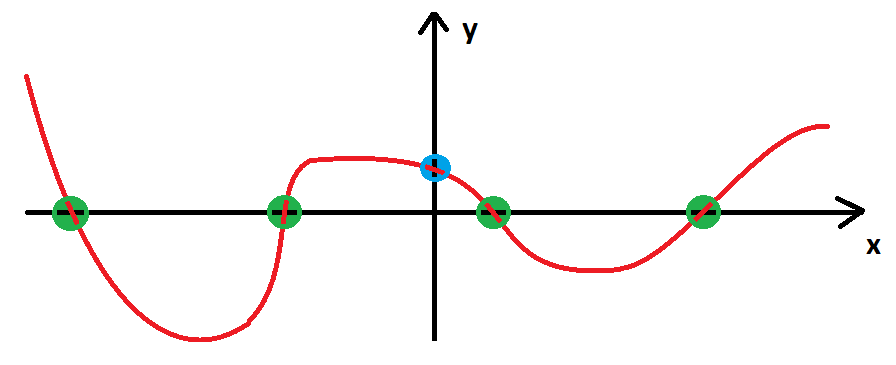
Zeleně vyznačené body jsou průsečíky s osou x, modře zobrazený bod je průsečík s osou y. Všimněme si, že každý zelený bod, tedy průsečík s osou x má y-ovou souřadnici rovnou nule. Tedy P_x=[x;0]. Pokud chceme zjistit x-ovou souřadnici, musíme do předpisu funkce dosadit za y nulu a vypočíst hodnotu x. Těchto průsečímů může být více, ale také žádný.
Modře vyznačený bod je průsečík s osou y. Všimněme si, že modrý bod má x-ovou souřadnici rovnou nule. Tedy P_y = [0;y]. Pokud chceme zjistit y-ovou souřadnici, musíme do předpisu funkce dosadit za y nulu a vypočíst hodnotu y. Tento průsečík může být buď jeden nebo žádný. Žádná z jiných možností nepřipadá v úvahu.
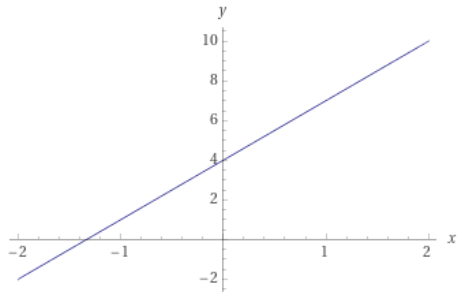
Příklad: Vypočti průsečíky s osami u funkce f: y=3x+4.
Průsečík s osou x:
y=3x+4 \\ 0=3x+4 \\ 3x=-4 \\ x=-\frac{4}{3}
Průsečík s osou y:
y=3x+4 \\ y=3 \cdot 0 +4 \\ y = 4
Průsečíky: P_x = [-\frac{4}{3};0], P_y = [0;4]
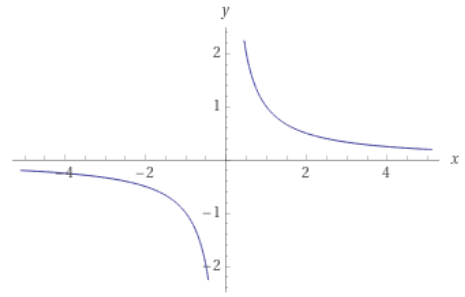
Příklad: Jsou případy, kdy průsečík s osou x nebo y neexistují, jako u funkce f:y=\frac{1}{x}.
Průsečík s osou x:
y = \frac{1}{x} \\ 0 = \frac{1}{x}
Vidíme, že dosazením libovolného čísla (kromě nuly) za x nikdy nedostaneme na pravé straně rovnice nulu. Průsečík s osou x tak neexistuje.
Průsečík s osou y:
y = \frac{1}{x} \\ y = \frac{1}{0}
Nula ve jmenovateli nemůže být, průsečík s osou y neexistuje.