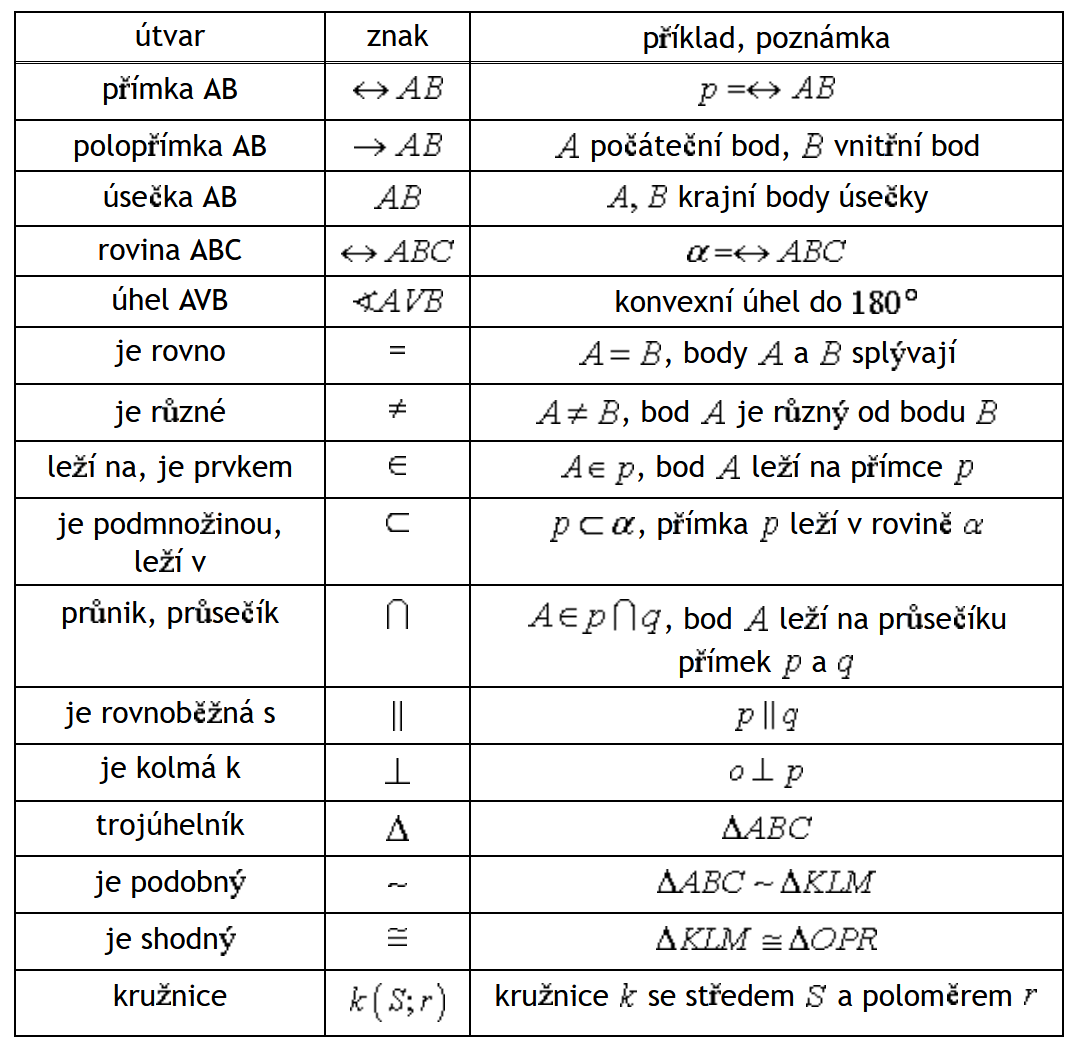
Základními útvary jsou:
- bod: značíme velkými písmeny A, B, S, ...
- přímka: značíme malými písmeny p, q, u, ...
- rovina: značíme malými řeckými písmeny \alpha, \beta, \gamma, ...
Pomocí těchto pojmů lze definovat další útvary:
- polopřímka: má daný jeden bod jako počátek (zapisuje se jako první, rozděluje přímku na dvě polopřímky) a druhý jako vnitřní bod, který určuje, o kterou polopřímku se jedná (určuje směr).
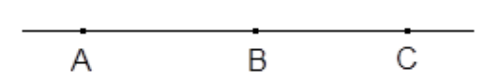
- úsečka: je dána dvěma krajními body, délka (velikost) úsečky A, B je vzdálenost jejích krajních bodů. Značíme \mid AB \mid .

A, B ... krajní body úsečky
S, C ... vnitřní body úsečky
S ... střed úsečky, \mid AS \mid = \mid BS \mid
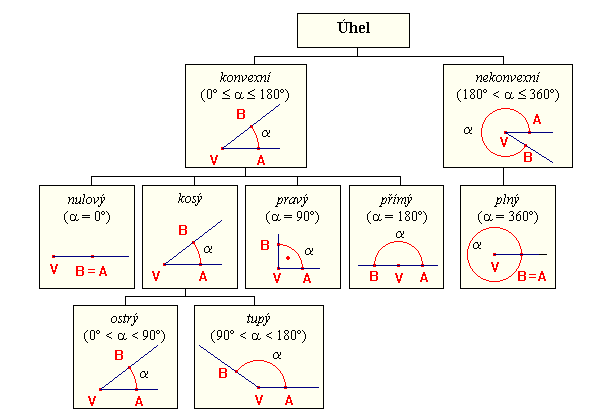
- konvexní útvar: jsou-li krajní body libovolné úsečky vnitřními body útvaru, jsou vnitřní body útvaru i všechny ostatní body této úsečky (celá úsečka leží uvnitř útvaru).
- Jiná definice: V geometrii je konvexní mnohoúhelník takový mnohoúhelník, jehož všechny vnitřní úhly jsou konvexní, tedy velikostně menší nebo rovny úhlu přímému (180 stupňů).
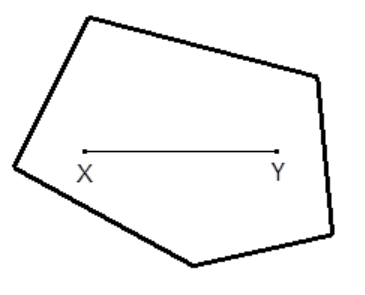
- nekonvexní útvar: existuje úsečka, jejíž krajní body jsou vnitřními body útvaru, ale některý vnitřní bod této úsečky není vnitřním bodem útvaru (část úsečky neleží uvnitř útvaru).
- Jiná definice: V geometrii je nekonvexní mnohoúhelník takový mnohoúhelník, jehož alespoň jeden vnitřní úhel je nekonvexní, tedy velikostně větší úhlu přímému (180 stupňů).
Úhel
Pojem úhlu patří k nejzákladnějším pojmům geometrie. Zajímavé je, že úhel můžeme definovat několika různými způsoby, z nichž má každý své opodstatnění.
Nejzákladnější definice říká:
Úhel je část roviny omezená dvěma polopřímkami se společným počátkem.
Při takto definovaném úhlu si však musíme uvědomit, že polopřímky VA a VB vymezují dva různé úhly, a to :
- konvexní úhel AVB s označením \measuredangle AVB
- nekonvexní úhel AVB s označením ___ AVB
- Bod V se nazývá vrchol úhlu AVB.
- Polopřímky VA a VB se nazývají ramena úhlu AVB.
- Úhly často zjednodušeně označujeme malými písmeny řecké abecedy.
Úhel zapisujeme písmeny řecké abecedy, např.\measuredangle \beta nebo pomocí tří bodů (např. \measuredangle AVB, přičemž první bod je bod ležící na počátečním rameni, druhý bod je vrchol a třetí bod je bod ležící na koncovém rameni daného úhlu.
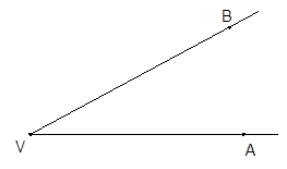
- \longmapsto VA ... počáteční rameno úhlu
- \longmapsto VB ... koncové rameno úhlu
- V ... vrchol úhlu
Osa úhlu
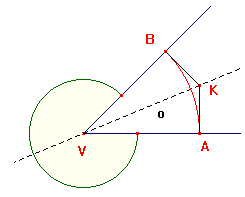
Ke každému úhlu náleží tzv. osa úhlu. Je to vlastně přímka, která rozděluje úhel na dvě shodné části - dva shodné úhly. Osu úhlu můžete vytvořit například tak, že úhel vystřižený z papíru přeložíte napůl.
Na obrázku je osa znázorněna jako přímka o. Osy úhlů kreslíme tenkou čerchovanou čarou.
Velikost úhlu
Velikost úhlu se považuje za veličinu, tudíž se k velikosti úhlu připojuje značka úhlové jednotky. Úhly se zpravidla měří v obloukové nebo stupňové míře. Více k obloukové míře v učivu 2. ročníku.
Velikost úhlu - základní jednotky:
- úhlový stupeň (zkráceně stupeň, značíme °)
- úhlová minuta (zkráceně minuta , značíme '); jedná se o \frac{1}{60} stupně
- úhlová vteřina (zkráceně vteřina, značíme ''); jedná se o \frac{1}{60} minuty
Platí:
- 1° = 60' = 3600"
- celý kruh (plný úhel) má velikost \alpha = 360°.
Počítat v takovéto nedesítkové soustavě jednotek není samozřejmě nic příjemného. Často bude potřebné uskutečňovat různé převody mezi stupni, minutami a vteřinami, proto by bylo vhodné si je procvičit. Tyto převody jsou poněkud zdlouhavé, avšak návrhy na měření úhlů v desítkové soustavě se dodnes v běžném životě neujaly. Jistým pokusem bylo zavedení tzv. setinné míry, ale i její používání je velmi omezeno.
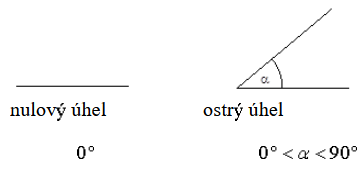
Názvy úhlů vzhledem k velikostem:
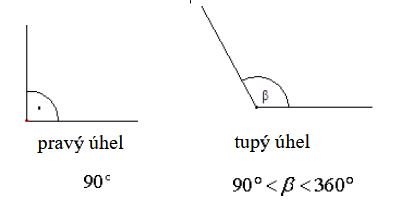
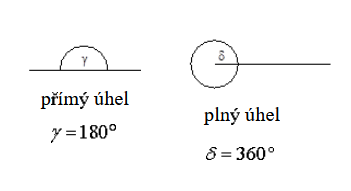
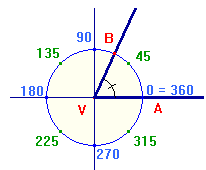
Orientace úhlu
Při operaci s úhly a při vkládání úhlů do soustavy souřadnic je důležitý kromě velikosti úhlu také směr odečtení úhlu. Musíme tedy zvolit vždy jedno rameno úhlu jako počáteční (v soustavě souřadnic většinou kladná poloosa x) a druhé rameno jako konečné. Při odečítání velikosti tohoto tzv. orientovaného úhlu postupujeme vždy od počátečního ramena ke konečnému.
- Proti směru hodinových ručiček - kladný úhel
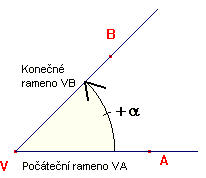
- Po směru hodinových ručiček - záporný úhel
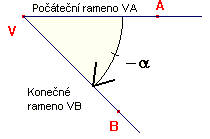
Nastane-li tedy situace, že máme odečítat větší úhel od menšího, výsledkem bude záporný úhel.
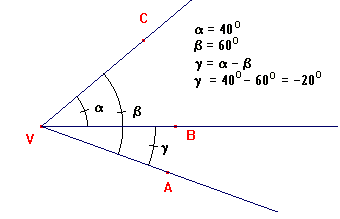
Názvy úhlů vzhledem k poloze - 1 uzel:
Styčné úhly: Styčnými úhly nazýváme dva úhly, jejichž součet velikostí je menší než velikost plného úhlu (180°) a jejichž dvě ramena splývají a zbývající dvě ramena leží ve vzájemně opačných polorovinách s hraniční přímkou obsahující společné rameno.
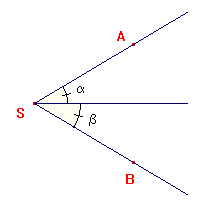
Vrcholové úhly: Vrcholovými úhly nazýváme úhly, jejichž vrcholy splývají a ramena jsou vzájemně opačné polopřímky. Vrcholové úhly jsou shodné.
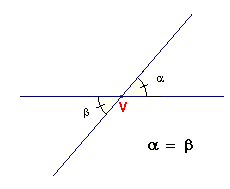
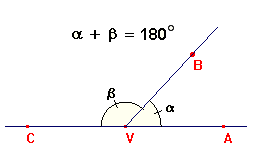
Vedlejší úhly: Vedlejšími úhly nazýváme styčné úhly, jejichž nesplývající ramena jsou vzájemně opačné polopřímky. Součet dvou vedlejších úhlů je přímý úhel.
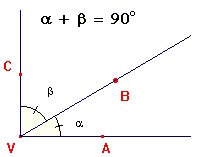
Doplňkové úhly: Dva úhly jež mají společné jedno rameno a jejichž grafickým součtem je úhel pravý, se nazývají doplňkové. Součet dvou doplňkových úhlů je pravý úhel.
Názvy úhlů vzhledem k poloze - 2 uzely:
Souhlasné úhly:
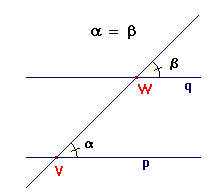
Střídané úhly:
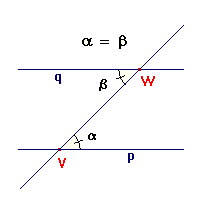
Střídavé a souhlasné úhly mají jedno společné rameno a druhá ramena rovnoběžná. Velikosti střídavých i souhlasných úhlů se vždy rovnají. Rozdíl mezi těmito typy dvojic úhlů je vidět na obrázku.
Sčítání a odčítání úhlů - graficky
Grafické sečtení úhlů a + b provedeme tak, že nejprve k jednomu rameni úhlu a přeneseme úhel \beta mimo úhel \alpha. To znamená, že se oba úhly nepřekrývají, pokud jejich součet nepřesáhl 360<sup>o</sup>. Jejich součet je tedy úhel, kretý vymezila jejich nesouhlasná ramena.
Při odečítání úhlů a - b postupujeme obdobně, pouze úhel \beta přeneseme dovnitř úhlu \alpha. Výsledný úhel opět vytyčují nespolečná ramena obou úhlů.
Pozor ! Jestliže a<b, musíme dát pozor na orientaci úhlu. Pokud se chcete těmto problémům vyhnout, počítejte raději rozdíl b - a.
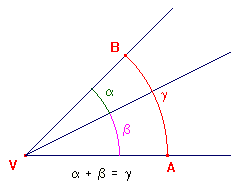
Sčítání a odčítání úhlů - početně
Ze stupňů na minuty
Při převodu velikosti úhlu na minuty musíme vědět, že 1°= 60'. Vynásobíme tedy stupně šedesáti a zbylé minuty k nim přičteme. Příklad: Převeďte 21° 15' na minuty.
21°15' = 21°\cdot 60 + 15' = 1 260' + 15' = 1 275'
Z minut na stupně
Při převodu velikosti úhlu z minut na stupně a minuty postupujeme přesně naopak než v předchozím příkladě. Příklad: Zapište úhel o velikosti 2421' ve stupních.
Vydělíme počet minut šedesáti a dostaneme hodnotu ve stupních:
2421' = 2421° : 60 = 40,35°
Potřebujeme-li výsledek ve stupních a minutách, musíme ještě hledat nejbližšího nižšího dělitele šedesáti. Tím je v našem případě číslo 2400.
2421' = 2400' + 21' = 2400 : 60° + 21' = 40°21'
Vyjádření úhlu desetinným číslem
Stačí si připomenout, že 1° = 3600''. To znamená že počet vteřin musíme tímto číslem vydělit. Příklad: Vyjádřete velikost úhlu 12° 15' 18'' desetinným číslem ve stupních.
12°15'18'' = 12° + 15°:60 + 18° : 3600 = 12° + 0,25° + 0,005° = 12,255°
Z desetinného čísla na stupně
Opačný postup je poněkud složitější, avšak budeme jej jistě potřebovat. Zkusme tedy převést např. 42,41° na stupně, minuty a vteřiny:
Oddělíme celé stupně: 42,41° = 42° + 0,41°
Desetinnou část vynásobíme šedesáti: 0,41° \cdot 60 = 24,6'
Opět oddělíme celou část a zapíšeme jako minuty: 42°24' + 0,6'
Vynásobíme desetinnou část minut: 0,6' \cdot 60 = 10''
Zapíšeme výsledek: 42,41° = 42° 24' 10''
Sčítání úhlů
Příklad: 12°30'10'' + 60°20'15'' = (12+60)° + (30+20)' + (10+15)' = 72°50'25''
Pozor, pokud by minuty nebo vteřiny překročili hodnotu 60, bylo by nutné je převést: 1°=60' a 1'=60''.
Příklad: 10°50'30'' + 40°29'40'' = (10+40)° + (50+29)' + (30+40)'' = 50°79'70''
Vidíme, že minuty i vteřiny překročili hodnotu 60. Proto je nutné je převést. Nejprve vyřešíme vteřiny:
70'' = 1' 10''
Dostáváme: 50°80'10''
Nyní je nutné převést ještě minuty, protože ty také přesáhly hodnotu 60.
80' = 1°20'
Výsledek příkladu tedy je: 51°20'10''
Odčítání úhlů
Zvýšenou pozornost budeme věnovat odčítání úhlů. V případě, že odčítáme menší číslo od většího, nenastane problém. Pokud bychom ale odečítali větší číslo od menšího, je nutné opět využít vztah mezi stupni, minutami a vteřinami.
Příklad: 50°40'-20°12' = (50-20)° + (40-12)' = 30°28'
Příklad: 40°15'25'' - 22°25'55''
Vidíme, že bychom odečítali 25'' - 55'' = -30''. Musíme provést úpravu vteřin v prvním čísle: 15'25'' = 14'85''
40°14'85'' - 22°25'55''
Stále bychom měli problém na místě minut. Provedeme druhou úpravu:
40°14'85'' = 39°74'85''
Pak dostáváme:
40°74'85'' - 22°25'55'' = (40-22)° + (74-25)' + (85-55)'' = 18°49'30''Příklady:
GÁL, Tomáš a Antonín KAMARÝT. Opakování středoškolské matematiky: příručka pro uchazeče o studium na vysokých školách zemědělských. 2., přeprac. a rozš. vyd. Praha: Státní zemědělské nakladatelství, 1965. Živočišná výroba (Státní zemědělské nakladatelství).
KUBÁT, Josef, Josef PILGR a Dag HRUBÝ. Sbírka úloh z matematiky pro střední školy: maturitní minimum. Praha: Prometheus, 1996. Učebnice pro střední školy (Prometheus). ISBN 80-7196-030-6.