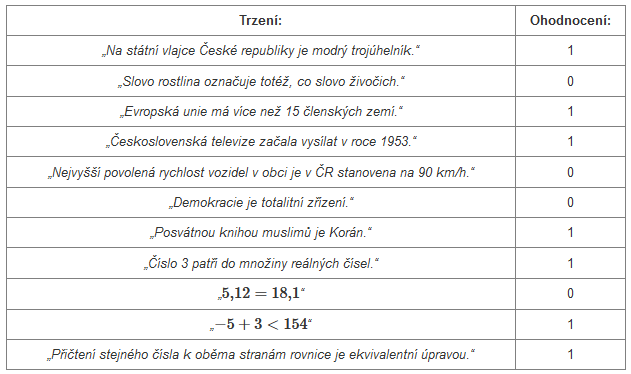
První termín z matematické logiky, kterým se budeme zabývat, je takzvaný výrok:
Definice: Za výrok budeme považovat jakékoli tvrzení, u kterého má smysl zabývat se otázkou, zda je či není pravdivé (podle toho pak výrok budeme nazývat pravdivým nebo nepravdivým).
Zároveň je nutné dodat, že tato tvrzení budeme zkoumat samostatně, bez souvislosti s případným kontextem. Každé tvrzení pro nás bude samostatným celkem. Je dobré si uvědomit, že není nutné okamžitě vědět, zda je dané tvrzení pravdivé nebo nepravdivé, abychom o něm řekli, že se jedná o výrok. Musí ale být smysluplné zabývat se otázkou pravdivosti tohoto tvrzení (v dalším textu si ukážeme tvrzení, kde to smysluplné není), jinak řečeno musí existovat cesta, jak se k pravdivosti tvrzení dobrat.
Výrok je tedy tvrzení, na které lze odpovědět ANO nebo NE. Co nás už ale nezajímá je fakt, zda je odpověď pravdivá či nepravdivá. Tedy výrok Venku prší je výrok bez ohledu na to, zda víme, zda venku prší nebo ne. Na Tento výrok vždy můžeme odpovědět ano / ne. Výrok není ale tvrzení Kolik je hodin? nebo Jdu domů!
Pravdivostní ohodnocení
Když o nějakém výroku výroku řekneme, že je pravdivý nebo nepravdivý, znamená to, že jsme tomuto výroku přiřadili pravdivostní ohodnocení.
Definice: Pravdivostní ohodnocení výroku říká, zda je výrok pravdivý či nepravdivý.
Pokud ohodnocuji výrok pravdivě, přiřadím mu hodnotu 1, pokud je výrok nepravdivý, přiřadím mu výrok 0.
Negace výroku
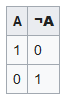
Definice: Negací výroku budeme rozumět takový výrok, který popírá pravdivost výroku původního.
Pokud tedy byl výrok ohodnocen 1, jeho negace bude 0. Pokud byl výrok ohodnocen 0, negace bude 1.
Značení: Mějme výrok a. Potom negace tohoto výroku se označuje \lnot{a} .

Tabulka pravdivostních hodnot:
Logické spojky
Jistě jste si všimli, že jsme se zatím zabývali jen jednoduchými větami. Jazyk matematické logiky ale potřebuje výroky spojovat a vytvářet tak větší celky, stejně jako běžná řeč. Avšak není to tak jednoduché – matematika musí být přesná, a tak i způsob spojování výroků musí být přesně nadefinován.
Ke spojování výroků se používají logické spojky. Pokud spojíme dva výroky pomocí logické spojky, výsledkem bude opět výrok. Můžeme tak vytvářet i velmi složité celky, které budou stále výrokem. Aby nějaké tvrzení bylo výrokem, musí odpovídat definici výroku. Jak je to tedy s těmito spojkami?
Když si vzpomeneme na definici výroku, zjistíme, že potřebujeme, aby u vzniklého celku mělo smysl zabývat se jeho pravdivostí. Logické spojky jsou navrženy právě tak, že přesně říkají, jaké bude pravdivostní ohodnocení výsledného výroku v závislosti na pravdivostním ohodnocení dílčích výroků, ze kterých je složen. Lze se tedy pravdivostí výsledného tvrzení nejen zabývat, ale pokud ji známe u dílčích výroků, můžeme ji i snadno určit.
Definice: Výroku, který vznikl právě spojením jiných výroků pomocí logických spojek, říkáme složený výrok.
Logické spojky
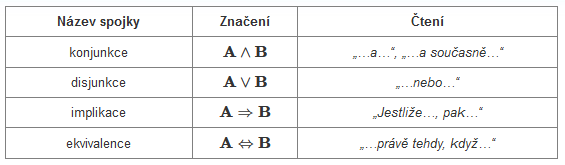
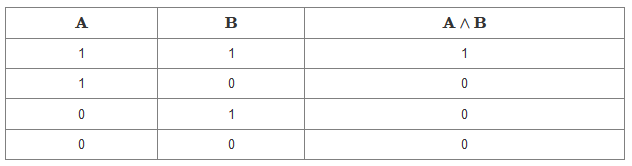
Konjunkce
Pod pojmem konjunkce si můžeme představit obdobu spojky „a“, kterou známe z běžné řeči, a také ji tak budeme číst. Její význam si osvětlíme na příkladu. Vezměme např. dva následující výroky:
- „V Lázních Jeseník právě prší.“
- „Ve Velimi právě fouká silný vítr.“
Po jejich spojení pomocí konjunkce (tedy vlastně spojky „a“) vznikne věta:
„V Lázních Jeseník právě prší a ve Velimi právě fouká silný vítr.“
Taková věta sice není stylisticky ideálním českým souvětím, její význam je však zřejmý. Chceme-li zapsat konjunkci dvou výroků a a b, používá se obvykle značení: a \land b.
Definice: Konjunkce je pravdivá právě tehdy, když jsou pravdivé oba spojované dílčí výroky. Jinak je nepravdivá.
Disjunkce
Další spojka, kterou se budeme zabývat, se jmenuje disjunkce a je to vlastně spojka „nebo“. V běžném jazyce se většinou spojka „nebo“ používá ve smyslu vylučovacím. V matematické logice je to trochu jinak, ukažme si to opět na příkladu. Budeme mít dva výroky:
- „K prvnímu nástupišti nádraží Praha–Holešovice včera ve 12:20 přijel rychlík Vsacan.“
- „Ke druhému nástupišti nádraží Praha–Holešovice včera ve 12:20 přijel vlak Eurocity Vindobona.“
Pokud tyto výroky spojíme pomocí disjunkce, získáme souvětí:
„K prvnímu nástupišti nádraží Praha–Holešovice včera ve 12:20 přijel rychlík Vsacan nebo ke druhému nástupišti nádraží Praha–Holešovice včera ve 12:20 přijel vlak Eurocity Vindobona.“
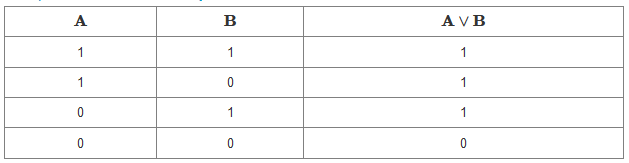
Definice: Disjunkce dvou výroků je pravdivá právě tehdy, když je pravdivý alespoň jeden ze spojovaných výroků.
Disjunkce dvou výroků a a b se zapíše pomocí znaku \lor: a \lor b.
Implikace
Dostáváme se ke spojce, jejíž pochopení může být náročnější. Nemá totiž jasný vzor v běžném jazyce. K prostému spojení dvou vět pomocí této spojky se používá sousloví „z toho plyne“. Avšak mnohem častěji se implikace do běžné řeči „překládá“ jako vazba „jestliže – pak“. Z toho by mohlo být vidět, že jsme se dostali k první spojce, u níž záleží na pořadí výroků. U konjunkce i disjunkce bylo jedno, zda jsme psali nejdříve první výrok a potom druhý nebo naopak. Spojením jsme získali výrok stejného významu i pravdivostního ohodnocení. Implikace se chová jinak, při změně pořadí výroků se změní nejen význam výsledného výroku, ale často i jeho pravdivostní ohodnocení. Zkusme si opět spojit dva výroky:
- „V Berouně prší.“
- „Hladina Berounky v Berouně stoupá.“
Teď je v uvedeném pořadí spojíme – zkusíme to oběma způsoby, které jsme si ukázali:
„V Berouně prší, z toho plyne, že hladina Berounky v Berouně stoupá.“
„Jestliže v Berouně prší, pak hladina Berounky v Berouně stoupá.“
Obě věty by se jistě daly ještě upravit, aby zněly o něco lépe, ale to není účelem našeho zkoumání. U spojení těchto výroků se zdá být lepší druhý způsob spojení, ale mohou nastat situace, kdy tomu bude naopak. Podívejme se, co se stane, prohodíme-li pořadí výroků:
„Jestliže hladina Berounky v Berouně stoupá, pak v Berouně prší.“
Věta získala zcela jiný význam. Zatímco původní věta říkala, že když prší, stoupne hladina vody, ta druhá nám tvrdí, že když stoupne voda, musí nutně v Berouně pršet (a to rozhodně nemusí být pravda). U implikací tedy musíme dbát na pořadí spojovaných výroků. A jak je to s pravdivostním ohodnocením implikace?
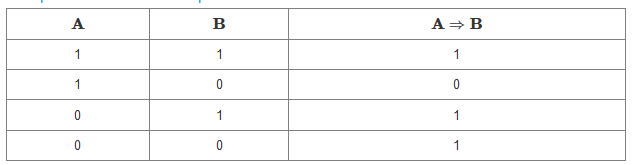
Definice: Implikace je pravdivá pravě tehdy, když jsou oba spojované výroky pravdivé nebo když je první výrok nepravdivý.
Neboli: Implikace není pravdivá jen v případě, že první výrok je pravdivý a zároveň druhý je nepravdivý.
Pro zachycení těchto informací pomocí tabulky pravdivostních hodnot opět potřebujeme značení. Ke spojení výroků a, b pomocí implikace se používá zvláštní dvojitá šipka: a \Rightarrow b .
Takový zápis můžeme číst mnoha způsoby:
- „Výrok A implikuje výrok B.“
- „Výrok B plyne z výroku A.“
- „Z výroku A plyne výrok B.“
- „Jestliže platí výrok A, pak platí výrok B.“
- „Jestliže A, pak B.“
Implikace je velmi často používaným výrokem v celé matematice, mnohdy totiž potřebujeme vyjádřit, že nějaký fakt plyne z jiného. Její pochopení je proto velmi důležité.
Ekvivalence
Další obtížnější spojkou je ekvivalence. Pokud výroky a, b spojíme pomocí ekvivalence, čteme takové spojení jedním z následujících způsobů:
- „A právě když B.“
- „A právě tehdy, když B.“
- „A tehdy a jen tehdy, když B.“
- „Výrok A je ekvivalentní s výrokem B.“
- „Výroky A a B jsou ekvivalentní.“
Značení takového spojení je podobné implikaci, ale šipku uděláme oběma směry: a⇔b.
A co vlastně znamená, že dva výroky jsou ekvivalentní? Stručně řečeno, nemusí být stejné, ale jejich „důsledek“ je stejný. Ukažme si to na příkladu:
- „Česká televize uvede pozítří ve 20:00 film Kolja.“
- „Veřejnoprávní televize v ČR bude pozítří v osm hodin večer vysílat film Kolja.“
Vidíme, že význam obou vět je stejný, jen bylo použito různých synonym. Nemusíme však zůstat u takto jednoduchého příkladu ekvivalence, protože pouhá záměna slov pomocí synonym by nám v matematice mnoho užitku nepřinesla. Ukažme si ještě jinou dvojici výroků.
- „Ludolfovo číslo je iracionální.“
- „Ludolfovo číslo nelze zapsat zlomkem.“
Zaměnili jsme dva termíny, které označují tutéž vlastnost čísla. I tentokrát bychom mohli hovořit o pouhém využití synonym. V matematice můžeme narazit i na podstatně složitější formulace, zatím ovšem nemáme dostatečné znalosti k jejich studiu.
Teď už bychom měli mít alespoň rámcovou představu o významu ekvivalence a můžeme se podívat na její pravdivostní ohodnocení:
Definice: Ekvivalence je pravdivá právě tehdy, když jsou oba výroky pravdivé nebo když jsou oba výroky nepravdivé.
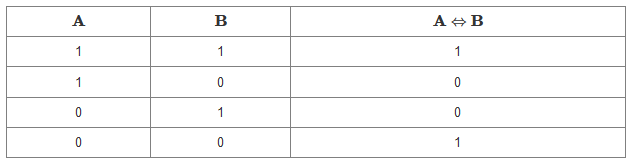
Z tabulky je dobře vidět, že u ekvivalence (stejně jako u konjunkce a disjunkce) je možné zaměnit pořadí výroků. Jedinou spojkou, se kterou jsme se zatím seznámili a u které je nutné dbát na pořadí výroků, je implikace.
Shrnutí