Monotónnost a prostá funkce
Monotónnost funkce vyjadřuje, kdy funkce roste nebo klesá, popř. neroste nebo neklesá. Mohou nastat čtyři základní typy:
Pozn.: U každé vlastnosti je uvedena definice, která není ale důležitá pro následné určování, zda je funkce rostoucí, klesající, ... Jedná se pouze o nadstavbu k lepšímu pochopení.
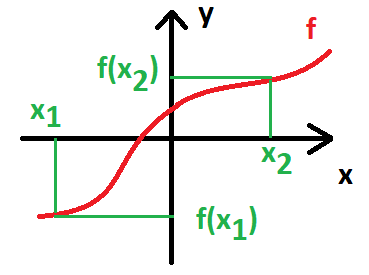
Funkce rostoucí (ryze monotónní)
Pokud je funkce rostoucí, pak každá další hodnota je větší než ta předcházející. Matematicky zapsáno:
\forall x_1, x_2 \in D_f: \ x_1 < x_2 \Rightarrow f(x_1) < f(x_2)
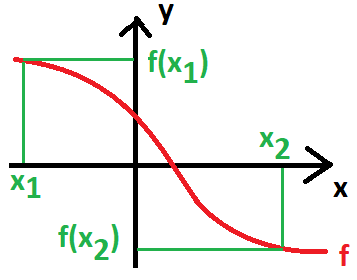
Funkce klesající (ryze monotónní)
Pokud je funkce klesající, pak každá další hodnota je menší než ta předcházející. Matematicky zapsáno:
\forall x_1, x_2 \in D_f: \ x_1 < x_2 \Rightarrow f(x_1) > f(x_2)
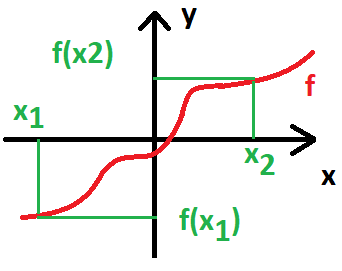
Funkce neklesající (monotónní)
Pokud je funkce neklesající, tak neklesá. Každá další hodnota je větší nebo rovna té předcházející. Nikdy se nestane, že by hodnota vlevo byla větší jak hodnota vpravo. Mohou být ale stejné.
\forall x_1, x_2 \in D_f: \ x_1 < x_2 \Rightarrow f(x_1) \le f(x_2)
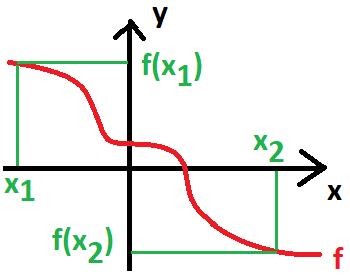
Funkce nerostoucí (monotónní)
Pokud je funkce nerostoucí, tak neroste. Každá další hodnota je menší nebo rovna té předcházející. Nikdy se nestane, že by hodnota vlevo byla menší jak hodnota vpravo. Mohou být ale stejné.
\forall x_1, x_2 \in D_f: \ x_1 < x_2 \Rightarrow f(x_1) \ge f(x_2)
Konstantní funkce
Pokud je funkce konstantní, tak je graf funkce rovnoběžný s osou x. Platí věty:
\forall x_1, x_2 \in D_f: \ x_1 < x_2 \Rightarrow f(x_1) \le f(x_2)
a zároveň
\forall x_1, x_2 \in D_f: \ x_1 < x_2 \Rightarrow f(x_1) \ge f(x_2)
Tedy konstantní funkce je funkcí monotónní, ale ne již ryze monotónní. Konstantní funkce je neklesající nebo nerostoucí, ale není rostoucí nebo klesající.
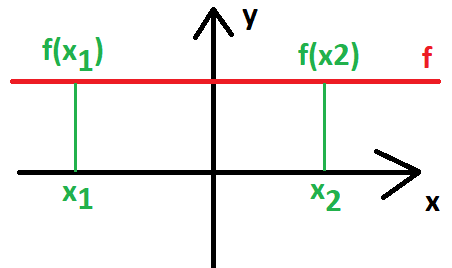
Funkce prostá
Funkce je prostá, pokud je pouze rostoucí nebo klesající na celém definičním oboru. Pokud je tedy funkce na celém definičním oboru ryze monotónní, pak můžeme říci, že je funkce prostá.
Důležitý je poznatek o celém definičním oboru, jelikož monotónnii můžeme určovat jako celek pro celý definiční obor, nebo můžeme říci, že například intervalu \langle -5;2 \rangle funkce roste, na \langle 2;8 \rangle funkce neklesá a na \langle 8;12 \rangle funkce klesá.
V případě definování vlastnosti je prostá / není prostá je podstatné, aby funkce byla ryze monotónní na celém definičním oboru funkce. Této vlastnosti je následně využito při tvorbě inverzní funkce.
Sudost a lichost funkce
Tato vlastnost býti sudá a býti lichá se zabývá symetrií funkce.
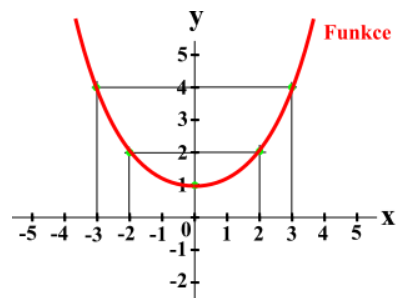
Sudá funkce: Funkce je sudá, pokud je souměrná podle osy y. Pokud bych nakreslil graf funcke na papír a papír ohnul v ose y, tak se křivka přenese z pravé strany papíru přesně na křivku na levé straně papíru.
\forall x \in D_f: \ f(x) = f(-x)
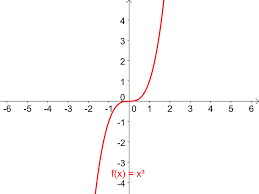
Funkce lichá: Funkce je lichá, pokud je souměrná podle počátku.
\forall x \in D_f: \ -f(x) = f(-x)
Jednotlivé definice (vztahy) sudosti a lichosti funkcí jsou důležité pro výpočet sudosti / lichosti funkce z předpisu funkce.
Příklad: Je funkce f: y=x^2 sudá, lichá nebo ani jedna?
f(x) = x^2 \\ f(-x) = (-x)^2 = x^2 \\ -f(x) = -x^2
Vidíme, že platí f(x) = f(-x), funkce je tedy sudá.
Dalším možným řešením je dosazení vhodných hodnot.
f(3) = 9 \\ f(2) = 4 \\ f(1) = 1 \\ f(-1) = 1 \\ f(-2) = 4 \\ f(-3) = 9
Opět vidíme, že platí f(x) = f(-x) a funkce je sudá.
Pozor, musí to platit pro všechny hodnoty z definičního oboru! Důležitý poznatek - aby funkce byla sudá nebo lichá, musí být její definiční obor také symetrický, tedy například od \langle -5;5 \rangle nebo ( -\infty ; \infty ). Nikdy ne ale například \langle -8;5 \rangle nebo \langle -5;5 ). V posledním příkladu by nám vadila krajní hodnota, jelikož interval je polouzavřený zleva.
Příklad: Je funkce g: y=2x sudá, lichá nebo ani jedna?
g(x) = 2x \\ g(-x) = 2 \cdot (-x) = -2x \\ -g(x) = -2x
Vidíme, že platí -g(x) = g(-x) a je splněna podmínka pro lichost funkce. Funkce je tedy lichá. Dalším řešením je dosazení vhodných hodnot:
g(3) = 6 \\ g(2) = 4 \\ g(1) = 2 \\ g(-1) = -2 \\ g(-2) = -4 \\ g(-3) = -6
Příklad: Je funkce h: y=2x-1 sudá, lichá nebo ani jedna?
h(x) = 2x-1 \\ h(-x) = 2 \cdot (-x)-1 = -2x-1 \\ -h(x) = -2x+1
Vidíme, že funkce není ani sudá ani lichá. Dosazením vhodných hodnot ověříme:
h(3) = 5 \\ h(2) = 3 \\ h(1) = 1 \\ h(-1) = -3 \\ h(-2) = -5 \\ h(-3) = -7
Poznámka: Určení sudosti / lichosti funkce podle předpisu je jednoznačný důkaz, že funkce je sudá nebo lichá. Dosazení vhodných hodnot je pouze orientační a může se stát, že pro libovolných 6 hodnot funkce vyjde jako sudá / lichá, nakonec tomu tak ale nebude. Jedná se o minimum příkladů, ale je nutné na toto pamatovat.
Dále je důležité zkontrolovat definiční obor, protože pokud krajní body nebudou symetrické (tedy stejné, jen s jiným znaménkem), tak také nemůžeme mluvit o sudosti / lichosti, i když dokážeme pomocí předpisu funkce a následných úprav, že funkce sudá nebo lichá je.
Omezenost funkce
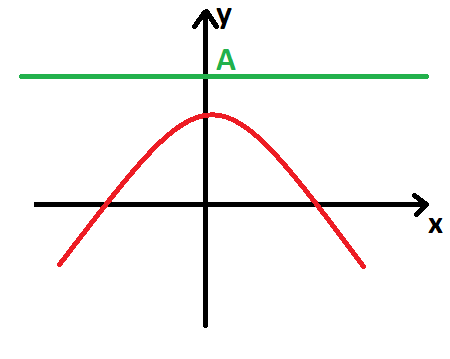
Funkce shora omezená: Řekneme, že funkce f je shora omezená, pokud existuje číslo A \in \R takové, že je větší jak všechny funkční hodnoty funkce f.
\forall x \in D_f \ \exists A \in \R: \ f(x) < A
Funkce zdola omezená: Řekneme, že funkce f je zdola omezená, pokud existuje číslo K \in \R takové, že je menší jak všechny funkční hodnoty funkce f.
\forall x \in D_f \ \exists K \in \R: \ f(x) > K
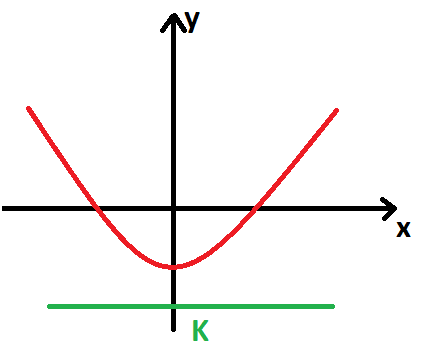
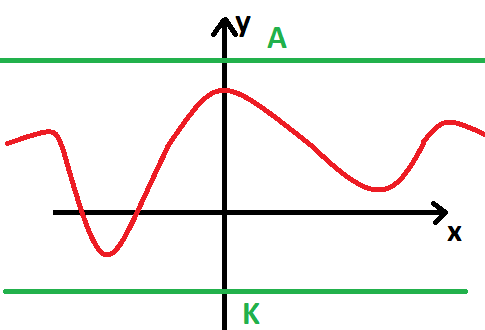
Funkce omezená: Řekneme, že funkce f je omezená, pokud je omezená zdola i shora zároveň.
\forall x \in D_f \ \exists A \in \R \ \exists K \in \R: \ K< f(x) < A
Extrémy funkce - maximum a minimum
Funkce f má v bodě M definičního oboru maximum, pokud je v tomto bodě M nejvyšší funkční hodnota ze všech funkčních hodnot (v okolí / na celém definičním oboru), které funkce má. Obdobně platí pro minimum.
Důležité je rozlišovat pojmy:
- Globální maximum - nejvyšší hodnota ze všech funkčních hodnot získaných z celého definičního oboru funkce.
\forall x \in D_f \ \exists M \in D_f: \ f(x) \le f(M)
- Globální minimum - nejnižší hodnota ze všech funkčních hodnot získaných z celého definičního oboru funkce.
\forall x \in D_f \ \exists M \in D_f: \ f(x) \ge f(M)
- Maximum (lokální maximum) - nejvyšší hodnota ze všech funkčních hodnot získaných z určitého intervalu I \subset D_f definičního oboru funkce.
\forall x \in I \subset D_f \ \exists M \in I: \ f(x) \le f(M)
- Minimum (lokální minimum) - nejnižší hodnota ze všech funkčních hodnot získaných z určitého intervalu definičního oboru funkce.
\forall x \in I \subset D_f \ \exists M \in I: \ f(x) \ge f(M)
Příklad: Vyšetři extrémy funkce, globální extrémy funkce, urči definiční obor a obor hodnot, rozhodni o omezenosti funkce.
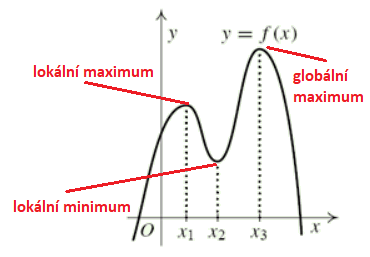
Definiční obor funkce D_f = \R, obor hodnot H_f = (-\infty ; f(x_3) \rangle Funkce f má v bodě x_1 lokální maximum, v bodě x_2 lokální minimum a v bodě x_3 globální maximum. Funkce nemá žádné globální minimum. Funkce je omezená shora.
Příklad: Urči maximum a minimum funkce.
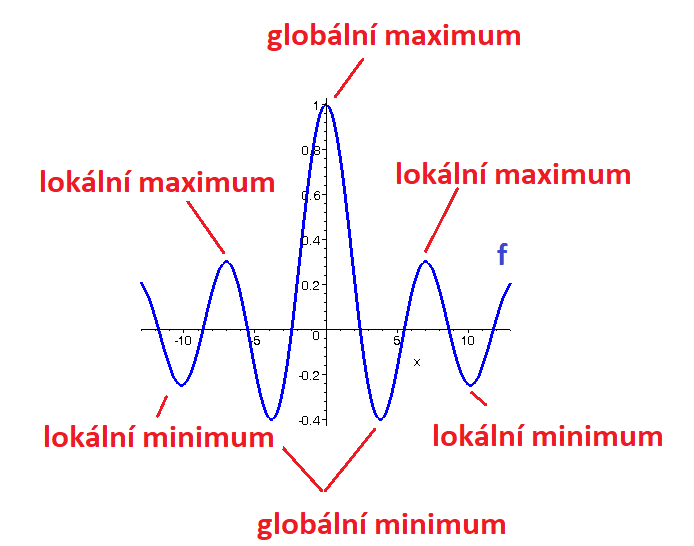
Lokální maxima:
\max_{x \in (-10;-5)} f(x) = 0,3 \\ \max_{x \in (5;10)} f(x) = 0,3 \\ \max_{x \in (-5;5)} f(x) = 1Globální maximum:
\max_{x \in D_f} f(x) = \max f(x) = 1Lokální minimum:
\min_{x \in (-15;-5)} f(x) = -0,2 \\ \min_{x \in (5;15)} f(x) = -0,2 \\ \min_{x \in (-10;0)} f(x) = -0,4 \\ \min_{x \in (0;10)} f(x) = -0,4Globální minimum
\min_{x \in D_f} f(x) = \min f(x) = -0,4Pediodicita
Funkce se nazývá periodická, pokud se po nějakém úseku opakuje. Příkladem periodické funkce je například takto vpadající funkce:
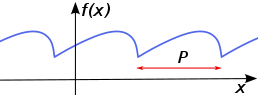
Vidíme, že oblouky jsou stejné. Můžeme si všimnout, že existuje určitý úsek (na obrázku oznčený p), který se postupně opakuje. Pokud bychom úseky vzali a přesunuly o úsek p doleva nebo doprava, přesunutá část překryje graf funkce.
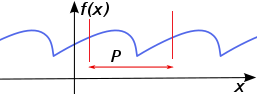
Opakující část (pro nás úsek označený p) se nazývá perioda p. Pokud bych v grafu funkce vybral jiný úsek jako periodu a kopíroval tento psek, vždy dostanu opět periodickou funkci. Délka periody ale zůstane vždy stejná!
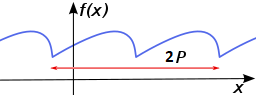
Můžeme také vzít větší část, každá další perioda ale bude násobkem té původní periody. Tedy například na agrafu níže opakuji periodu označenou 2p, která vznikla sloužením dvou po sobě jdoucích úúseků o délce p.
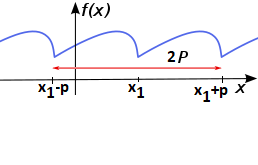
Definice: \forall x \in D_f \ \exists p \in \R : \ f(x_1) = f(x_1+p)=f(x_1-p
Periodické funkce jsou v drtivé většině funkce goniometrické, tedy funkce sinus, cosinus, tangens a cotangens. Příkladem periodické funkce je ale také například funkce konstantní.
Jak tedy poznat periodickou funkci? Stačí z grafu / ze zápisu vyčíst, že graf se po určitém úseku stále opakuje.