Tři množiny
Až doposud jsme si ukázali práci s Vennovými diagramy i s množinovými operacemi pouze pro dvě množiny. Ovšem v praxi se setkáváme i s podstatně většími počty množin. I na nich můžeme postupně provádět množinové operace (tak jako můžeme např. postupně sečíst tři čísla) a také pro ně můžeme použít Vennovy diagramy. Vennův diagram – jak jsme si již řekli – lze vytvořit pro libovolný konečný počet množin, my si však v této práci většinou vystačíme s diagramem pro dvě nebo pro tři množiny:
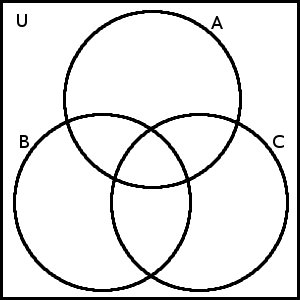
Tento diagram je opět univerzální a opět jej využijeme k ověřování různých pravidel pro práci s množinami. Zkusme například zjistit, zda je operace průniku asociativní, tedy zda platí (A \cap B) \cap C = A \cap (B \cap C).
Zakreslíme nejdříve levou stranu, tj. začneme množinou A \cap B:
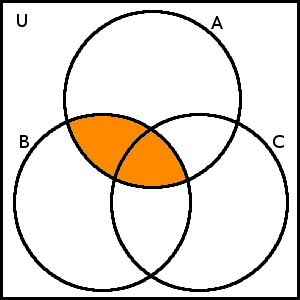
Co bude výsledným průnikem je asi zřejmé, přesto si však ještě vyšrafujme množinu C:
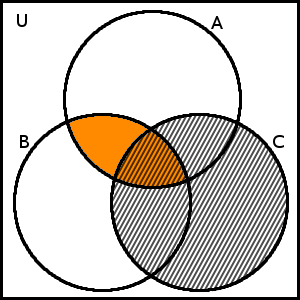
Výsledným průnikem je množina, která je na obrázku výše podbarvena i vyšrafována, tedy (A \cap B) \cap C
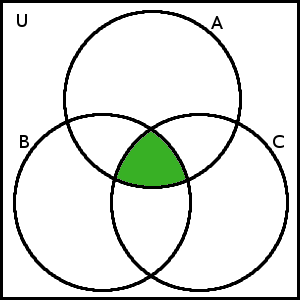
Nyní se podívejme na pravou stranu rovnosti. Nejprve zakreslíme množinu B\cap C:
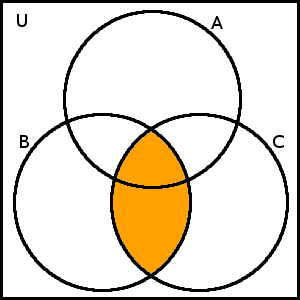
Vyšrafujeme množinu A.
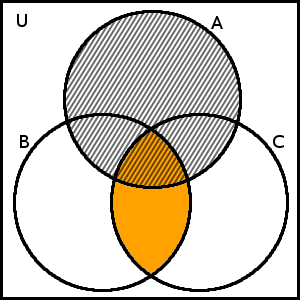
Výsledným průnikem je opět množina, která je na obrázku výše podbarvená oranžovou barvou a zároveň vyšrafovaná, tedy A\cap(B \cap C):

Pro levou i pravou stranu jsme získali stejný diagram, rovnost tedy platí. Z toho plyne, že operace průniku je asociativní. Pokud budeme postupně provádět několik průniků, nemusíme tedy používat závorky, místo (A \cap B) \cap C můžeme rovnou psát A \cap B \cap C.
Toto platí i pro sjednocení, tj. operace sjednocení je asociativní. Ověření tohoto pravidla zde provádět nebudeme, avšak je to vhodná příležitost k procvičení.
iž při zavádění operací sjednocení a průniku jsme si ukázali, že tyto operace jsou komutativní. Nyní víme, že jsou také asociativní, a tak můžeme zapsat např. následující rovnosti platící pro libovolnou trojici množin:
A \cap B \cap C = A \cap C \cap B = B \cap A \cap C = B \cap C \cap A = C \cap B \cap A = C \cap A \cap B A \cup B \cup C = A \cup C \cup B = B \cup A \cup C = B \cup C \cup A = C \cup B \cup A = C \cup A \cup BPodobné rovnosti bychom mohli psát také pro čtveřice množin, pětice,… Zkrátka s průnikem a sjednocením konečného počtu množin můžeme zacházet podobně jako se sčítáním a násobením u čísel. U čísel však platí také tzv. distributivní zákon – platí jeho obdoba i u množin? Zkusme to odvodit s využitím Vennových diagramů.
Máme ověřit, že platí A \cap (B \cup C)=(A \cap B)\cup(A \cap C), neboli že platí distributivnost průniku vůči sjednocení. Začneme nejdříve levou stranou rovnosti, zakreslíme nejprve množinu B \cup C a množinu A, potom zachytíme jejich průnik:
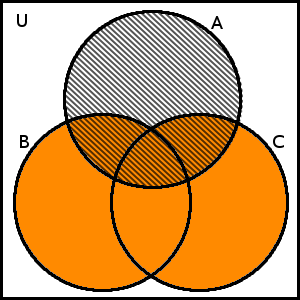
B \cup C a množinu A
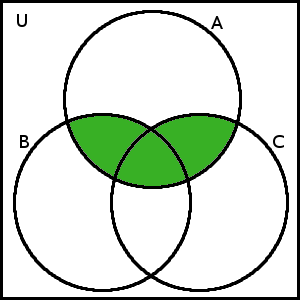
A \cap (B \cup C)
Zbývá znázornit pravou stranu rovnosti, tj. nejdříve množiny A \cap B, A \cap C a potom jejich sjednocení:
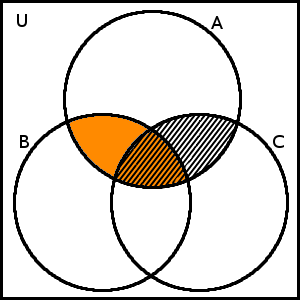
A \cap B a množina A \cap C

(A \cap B) \cup (A \cap C)
Vybarvené oblasti ve výsledných diagramech jsou opět shodné, rovnost A \cap (B \cup C) = (A \cap B) \cup (A \cap C) platí pro libovolné tři množiny A, B, C.
Tento vztah platí i v případě, že zaměníme průniky a sjednocení, tj. budeme-li uvažovat rovnost A \cup (B \cap C) = (A \cup B) \cap (A \cup C). Postup ověření je podobný jako v předchozím případě, proto si je nebudeme znovu ukazovat. Je to však dobré cvičení!
Příklady k procvičení: 24.10 (pouze příkady, kde se vyskytuje pouze průnik a nebo sjednocení); 24.18;
KRIEGELSTEIN, Eduard. Sbírka úloh z matematiky pro střední průmyslové školy a střední zemědělské technické školy. 10. vyd. Praha: Státní pedagogické nakladatelství, 1965.