Dříve než se pustíme do složitějších operací s množinami, seznámíme se s nástrojem, který nám umožní si mnoho poznatků jednoduše ukázat pomocí grafického znázornění - Vennovy diagramy, které představil v 19. století anglický vědec a kněz John Venn.
Vennův diagram umožňuje zaznamenat libovolný konečný počet množin tak, že rovnou zachytíme všechny přípustné možnosti rozložení prvků a můžeme tak na stejném diagramu modelovat různé situace. My budeme nejčastěji používat Vennův diagram pro dvě nebo pro tři množiny, pro velké počty množin jsou tyto diagramy již poměrně nepřehledné.
Ve Vennových diagramech se množiny zachycují jako část roviny ohraničená uzavřenou křivkou, v jednoduchých případech stačí kruh (tedy část roviny ohraničená kružnicí). Někdy se však používají i složitější tvary. Vennův diagram pro dvě množiny je vidět na následujícím obrázku:
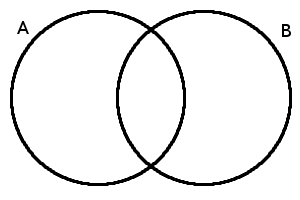
Dříve než si začneme ukazovat, jak na tomto diagramu vypadají jednotlivé situace a operace, bychom si měli říci, že obvykle při práci s množinami uvažujeme jen určitou skupinu prvků. Pokud např. vyjadřujeme nějaké operace s reálnými čísly pomocí množin, budeme v těchto množinách pracovat jen s reálnými čísly a prvky jako skleněný hrneček z nějaké skříňky nebo lachtan z liberecké ZOO jsou nám v takové situaci lhostejné. Obvykle tedy při konkrétní práci s množinami uvažujeme nějakou základní množinu (universum, funfamentální množina), ze které budeme prvky vybírat a množiny, s nimiž pracujeme, jsou potom jejími podmnožinami. V našem příkladu s reálnými čísly by touto základní množinou byla právě množina všech reálných čísel \R. Nejčastěji však budeme základní množinu značit U. Ve Vennově diagramu tuto množinu obvykle naznačujeme jako obdélník, uvnitř něhož jsou jednotlivé množiny – ukažme si předchozí Vennův diagram doplněný o základní množinu U:
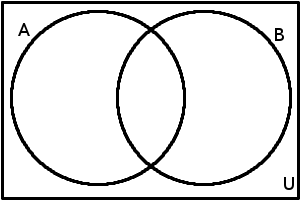
Nyní, když máme zavedenu základní množinu, můžeme některé vztahy a operace mezi množinami doplnit symbolickým zápisem, abychom si ukázali použití symbolů, jako jsou kvantifikátory nebo logické spojky, i pro účely této kapitoly. První takový zápis najdeme níže u následujícího obrázku. Tento obrázek ukazuje, jak Vennovým diagramem zachytit fakt, že množina je podmnožinou jiné množiny, konkrétně situaci, kdy B\subseteq A :
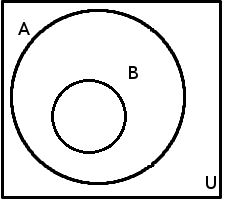
B\subseteq A \iff (\forall x \in U:x \in B \Rightarrow x\in A )
Sjednocení množin
Sjednocení množin označujeme symbolem \cup, tedy sjednocení množin A aB označíme klasicky: A \cup B.
Sjednocením množin A a B vznikne nová množina, která bude obsahovat všechny prvky z množiny A a také všechny prvky z množiny B.
Definice: A \cup B = \{x|x \in A \lor x \in B \}
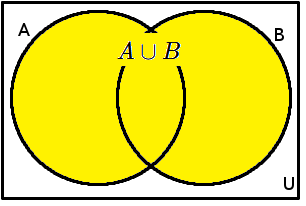
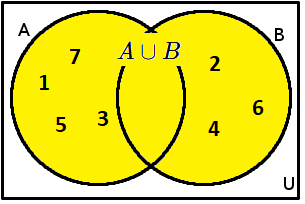
Ukázkový příklad: Mějme dvě množiny A=\{1;3;5;7\}, B=\{2;4;6\}. Sjednocením vznikne množina:
A \cup B=\{1;2;3;4;5;6;7\}.
Výsledná množina obsahuje prvky obou množin.
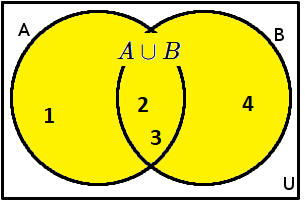
Další příklad: A=\{1;2;3\}, B=\{2;3;4\}. Sjednocením dostaneme: A \cup B = \{1;2;3;4\}. Prvky 2 a 3 nebudou ve výsledné množině dvakrát, protože množina neobsahuje jeden prvek vícekrát.
Další vlastnosti:
- Pokud sjednotíme dvě stejné množiny, dostaneme zase tutéž množinu.
A \cup A = A
- Sjednocení je komutativní, nezáleží na pořadí.
A \cup B = B \cup A
- Prázdná množina neobsahuje žádný prvek, takže není co sjednocovat.
A \cup \varnothing = A
Průnik množin
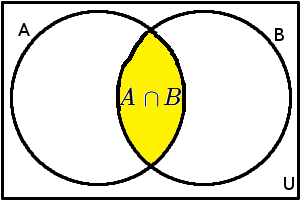
Průnikem dvou množin A a B vznikne nová množina, která bude obsahovat prvky, které mají ty dvě množiny společné. Přesněji bychom řekli, že nová množina bude obsahovat prvky, které náleží do A a zároveň náleží do B. Průnik označujeme symbolem \cap.
Definice: A \cap B = \{x|x \in A \land x \in B\}
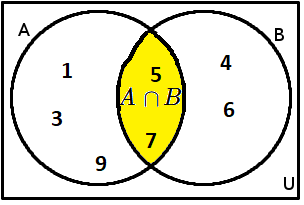
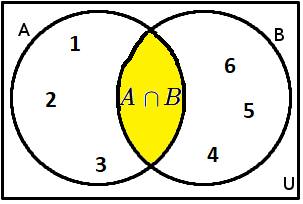
Příklad: A=\{1;3;5;7;9\}, B=\{4;5;6;7\}. Průnik je roven A \cap B = \{5;7\}.
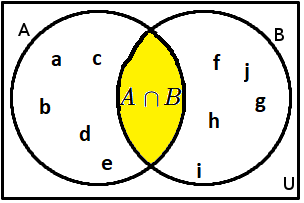
Další příklad: A=\{a;b;c;d;e\}, B=\{f;g;h;i;j\}. Průnik je roven: A \cap B = \varnothing . Tyto množiny nemají žádný společný prvek, takže průnikem je prázdná množina.
Další vlastnosti:
- Průnikem dvou stejných množin dostaneme zase stejnou množinu.
A \cap A=A
- Průnik je komutativní, nezáleží na pořadí.
A \cap B = B \cap A
- Prázdná množina neobsahuje žádný prvek, takže určitě nemá žádný stejný prvek jako množina A.
A \cap \varnothing = \varnothing
Disjunktní množiny
Dvě množiny nazveme disjunktní, pokud nemají žádný společný prvek. Tedy například množiny A=\{1;2;3\} a B=\{4;5;6\} .
Platí tedy A \cap B = \varnothing
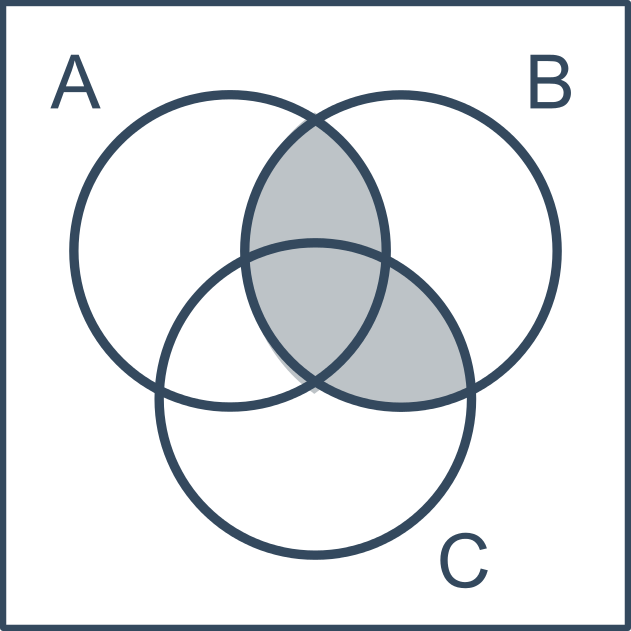
Příklad užití diagramu pro 3 množiny: A \cap (B \cup C)
Ukázkové příklady k pochopení pojmů:
- Uvažujme nějakou kuchyňskou skříňku s nádobím. Řekněme, že množina A je množina všech hrnečků ve skříňce, množinou B je pak množina všeho skleněného nádobí ve skříňce. Množina A \cap B je pak množina všech skleněných hrnečků ve skříňce. Pokud v ní žádné skleněné hrnečky nejsou, jsou množiny A a B disjunktní.
- Mějme množiny A=\{1;2;3;4;5;6\}, B=\{3;6;8;9\}. Pak A \cap B = \{3;6\}.
- A=\{-1;2;3;4;5;6\}, B=Q . Pak A \cap B = \{-1;2;3;4;5;6\}=A
- A=\{1;2;3;6\}, B=\varnothing. Prázdná množina neobsahuje žádné prvky, a tak nemůže mít s jinou množinou nějaký společný prvek.
- Předchozí příklad lze zobecnit na průnik libovolné množiny a prázdné množiny. Ten je totiž v takovém případě vždy prázdný. Neboli, pro libovolnou množinu A platí: A \cap \varnothing = \varnothing .
- Podobně se můžeme zamyslet nad tím, jak je to s průnikem množiny a její podmnožiny. Tím bude právě ona podmnožina - tedy: A \subseteq B \rightarrow A \cap B = A .
- Průnikem libovolné množiny se sebou samou je opět sama tato množina, množiny zúčastněné v tomto průniku mají společné právě všechny prvky: M \cap M = M .
- Operace průnik a sjednocení jsou komutativní. Vybíráme vždy prvky společné pro obě množiny a je lhostejné, u které začneme. Pro libovolné dvě množiny A a B platí: A \cap B = B \cap A.
Příklady k procvičení - vypočtěte příklady 24.3 až 24.4 a 24.6 až 24.7. Příklady 24.8, 24.9 vynechte.
KRIEGELSTEIN, Eduard. Sbírka úloh z matematiky pro střední průmyslové školy a střední zemědělské technické školy. 10. vyd. Praha: Státní pedagogické nakladatelství, 1965.