Trigonometrie je oblast matematiky, která se zabývá úlohami, kde se vyskytuje trojúhelník. Nemusí se ale jednat o trojúhelník pravoúhlý. Trojúhelník může být obecný a na tyto trojúhelníky se zaměříme.
Odvození Sinové věty
Mějme libovolný \triangle ABC a označme k jednotlivým vrcholům úhly \alpha, \beta, \gamma. Jelikož trojúhelník není pravoúhlý, pak nemůžeme aplikovat žádné goneometrické funkce. Ty umíme aplikovat pouze v trojúhelníku, který je pravoúhlý.
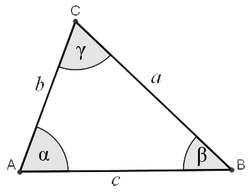
Prvním krokem v odvození Sinové věty je vytvoření si z tohoto obecného trojúhelníku trojúhelník pravoúhlý. Můžeme spustit výšku z vrcholu C. Patu výšky označme P. Získali jsme stranu CP a dále pak dva pravoúhlé trojúhelníky APC a BCP.
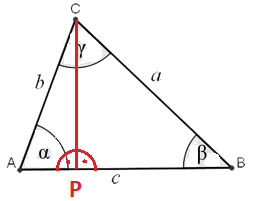
Vidíme, že můžeme použít sinus úhlu {katex]\alpha[/katex]:
\sin{(\alpha)} = \frac{|CP|}{b}
\sin{(\alpha)} \cdot b = |CP|
Máme ale ještě druhý pravoúhlý trojúhelník:
\sin{(\beta)} = \frac{|CP|}{a}
\sin{(\beta)} \cdot a = |CP|
Vyjádřil jsem si výšku |CP| dvěma různými způsoby. Platí, že oba tyto výrazy se sobě musí rovnat:
\sin{(\beta)} \cdot a = \sin{(\alpha)} \cdot b
Obě strany rovnice vydělím součinem ab
\frac{\sin{(\beta)} \cdot a}{ab} = \frac{\sin{(\alpha)} \cdot b}{ab}
\frac{\sin{(\beta)}}{b} = \frac{\sin{(\alpha)}}{a}
Sinová věta nám říká, že poměr všech délek stran a hodnto sinů jim protilehlých úhlů je v daném obecném (!) trojúhelníku konstatní.
Pokud bychom stejným způsobem využili úhel \gamma, získali bychom vztah:
\frac{\sin{(\beta)}}{b} = \frac{\sin{(\alpha)}}{a}=\frac{\sin{(\gamma)}}{c}
nebo lze zapsat Sinovu větu převráceným způsobem (vždy jde o poměr, mohu převrátit).
\frac{b}{\sin{(\beta)}}=\frac{a}{\sin{(\alpha)}}=\frac{c}{\sin{(\gamma)}}
Vidíme, že dříve jsme byli omezeni pouze na pravoúhlé trojúhelníky. Nyní jsme ale dostali výraz, který platí pro trojúhelníky obecné. Využití této věty je v případě, kdy známe v obecném trojúhelníku stranu a dva úhly nebo úhel a dvě strany. Ukažme si příklad:
Příklad: Mějme \triangle ABC, jehož strany mají délku a = 5 cm a c = 7 cm, úhel \alpha = 40°. Dopočítejte ostatní úhly a strany.
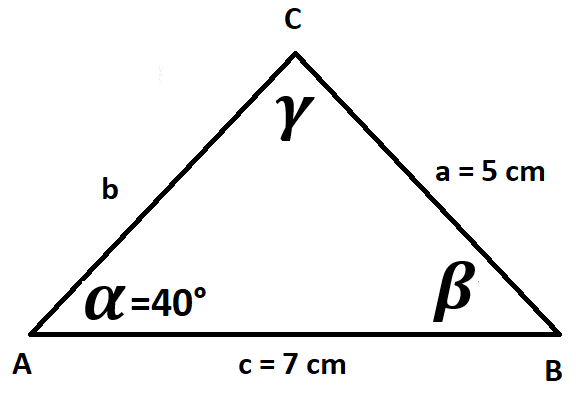
\frac{\sin{(\alpha)}}{a}=\frac{\sin{(\gamma)}}{c}
\frac{\sin{(40°)}}{5}=\frac{\sin{(\gamma)}}{7}
\frac{\sin{(40°)}}{5} \cdot 7=\sin{(\gamma)}
\frac{0,64}{5} \cdot 7=\sin{(\gamma)}
\sin{(\gamma)}=0,46
\gamma = \arcsin{(0,46)}
\gamma = 27,33°
Víme, že součet úhlů v trojúhelníku je 180°. Pak tedy:
\beta = 180° - 40° - 27,33° = 112,67°
Chybí nám ještě vypočítat strana b, kteroubychom opět vypočítali pomocí Sinovi věty. Pozor, nelze užít Pythagorovu větu!!! Nejedná se o pravoúhlý trojúhelník.
Příklady: