Mnohostěny
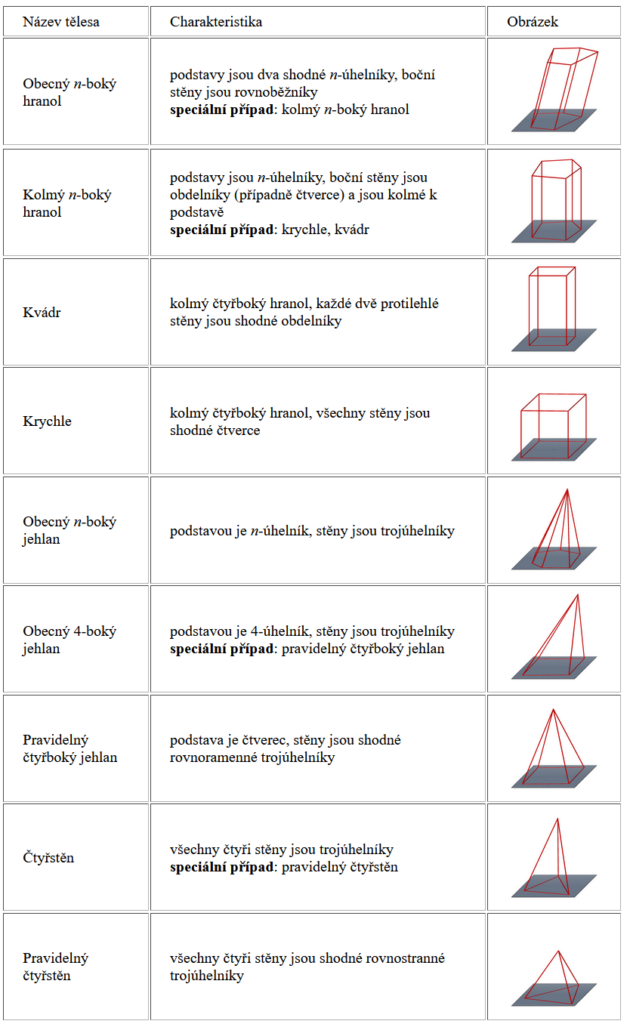
Řezy těles rovinou
Řezem tělesa rovinou nazýváme průnik roviny a tělesa.
My si ukážeme kontrukci řezu pomocí tří základních vět a jejich důsledků:
Věta 1: Leží-li dva různé body v rovině, pak přímka jimi určená leží také v této rovině.
Důsledek 1: Leží-li dva různé body roviny řezu v rovině některé stěny, leží v rovině této stěny i jejich spojnice. Průnik spojnice a stěny je jednou stranou řezu.
Věta 2: Dvě rovnoběžné roviny protíná třetí rovina ve dvou rovnoběžných přímkách.
Důsledek 2: Jsou-li roviny dvou stěn rovnoběžné a přitom různoběžné s rovinou řezu, jsou průsečnice roviny řezu s rovinami těchto stěn rovnoběžné.
Věta 3: Jsou-li každé dvě ze tří rovin různoběžné a mají-li tyto tři roviny jediný společný bod, procházejí tímto společným bodem všechny tři průsečnice.
Důsledek: Průsečnice rovin dvou sousedních stěn (tj. stěn se společnou hranou) s rovinou řezu a přímka, v níž leží společná hrana, se protínají v jednom bodě.
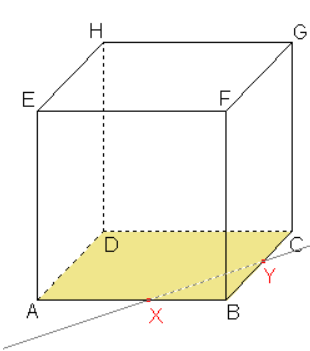
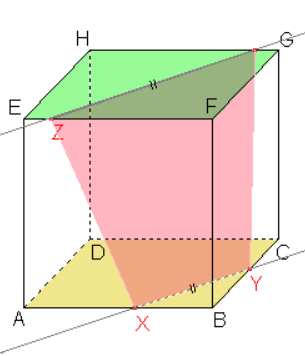
Příklad č. 1: Sestrojte řez krychle ABCDEFGH rovinou BGX, kde bod X je střed hrany AE.
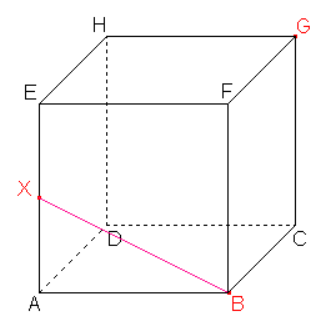
Dle důsledku 1 leží body B, \ X roviny řezu leží v rovině přední stěny, tedy i jejich spojnice leží v rovině této stěny. Průnik spojnice a stěny je jednou stranou řezu.
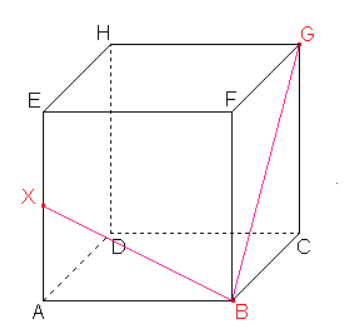
Dle důsledku 1 body B, \ G roviny řezu leží v rovině pravé boční stěny, tedy i jejich spojnice leží v rovině této stěny. Průnik spojnice a stěny je další stranou řezu.
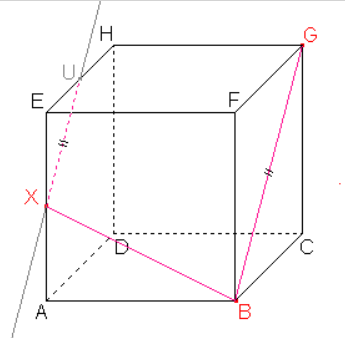
Sestrojíme bod U a stranu řezu X, \ U v boční stěně A, \ D, \ E dle důsledku 2: Roviny bočních stěn jsou rovnoběžné a přitom různoběžné s rovinou řezu, proto jsou průsečnice roviny řezu s rovinami těchto stěn rovnoběžné.
Můžeme tedy sestrojit rovnoběžku ke straně řezu B, \ G procházející bodem X. Průnik rovnoběžky a hrany E, \ H je hledaný bod U a úsečka X, \ U je stranou řezu.
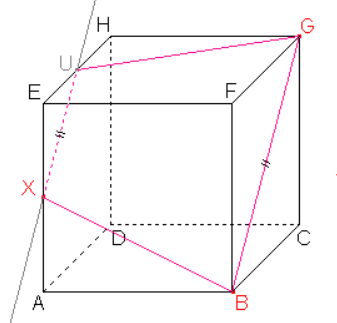
Dle důsledku 1: Body G, \ U roviny řezu leží v rovině horní stěny, tedy i jejich spojnice leží v rovině této stěny. Průnik spojnice a stěny je další stranou řezu.
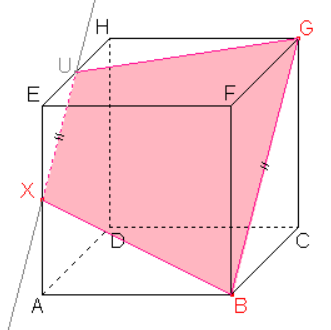
Nyní známe všechny vrcholy a strany mnohoúhelníku, který je řezem daného tělesa.
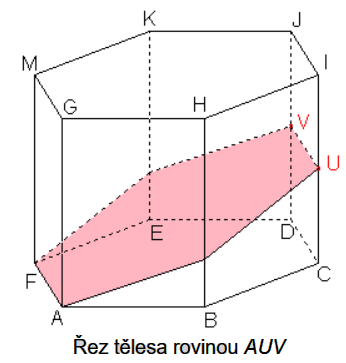
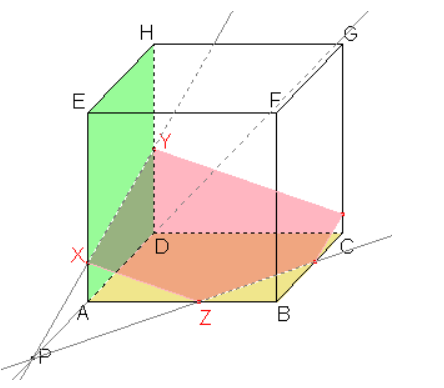
Příklad č. 2: Sestrojte řez kosého čtyřbokého hranolu ABCDEFGH, jehož podstava je lichoběžník, rovinou XYZ, kde bod X leží na hraně DH, bod Y leží na hraně GH, bod Z leží na hraně BF.
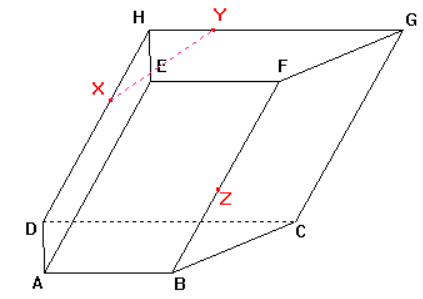
Dle důsledku 1 body X, \ Y roviny řezu leží v rovině zadní stěny, tedy i jejich spojnice leží v rovině této stěny. Průnik spojnice a stěny je stranou řezu.
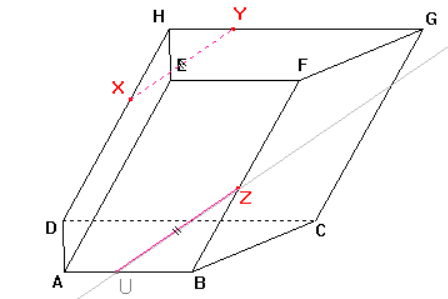
Sestrojíme bod U a stranu řezu ZU v přední stěně ABF dle důsledku 2: Roviny přední a zadní stěny jsou rovnoběžné a přitom různoběžné s rovinou řezu, proto jsou průsečnice roviny řezu s rovinami těchto stěn rovnoběžné.
Můžeme tedy sestrojit rovnoběžku ke straně řezu XY procházející bodem Z. Průsečík rovnoběžky a hrany AB je hledaný bod U a úsečka ZU je stranou řezu.
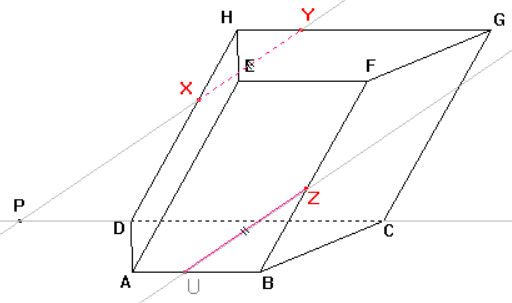
Dle důsledku 3 se průsečnice rovin zadní stěny a dolní podstavy, které jsou sousední, s rovinou řezu a přímka, v níž leží společná hrana těchto stěn, protínají v jednom bodě.
Sestrojíme tedy přímku danou body CD, v níž leží společná hrana zadní stěny a dolní podstavy, a průsečnici roviny řezu a zadní stěny, kterou je přímka XY. Bod P je průsečíkem přímky CD a přímky XY.
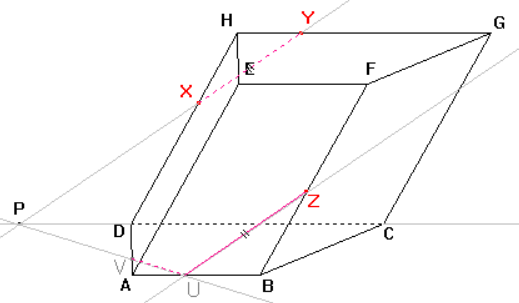
Dle důsledku 3 je bod P průsečíkem přímek CD,\ XY a přímky PU, která je průsečnicí roviny řezu a dolní podstavy. Nyní můžeme sestrojit průsečík V přímky PU a hrany AD a stranu řezu UV.
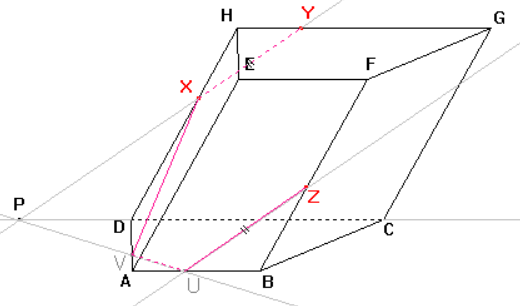
Dle důsledku 1: Body X, \ V roviny řezu leží v rovině boční stěny, tedy i jejich spojnice leží v rovině této stěny. Průnik spojnice a stěny je další stranou řezu.
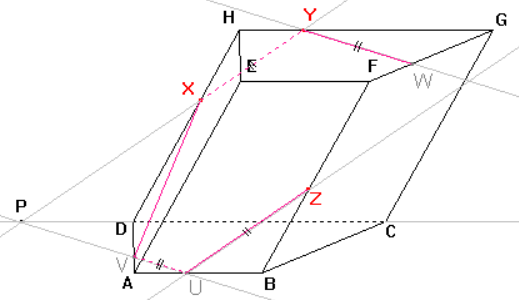
Sestrojíme bod W a stranu řezu YW v horní podstavě EFG dle důsledku 2: Roviny dolní a horní podstavy jsou rovnoběžné a přitom různoběžné s rovinou řezu, proto jsou průsečnice roviny řezu s rovinami podstav rovnoběžné.
Můžeme tedy sestrojit rovnoběžku ke straně řezu UV procházející bodem Y. Průsečík rovnoběžky a hrany FG je hledaný bod W a úsečka YW je stranou řezu.
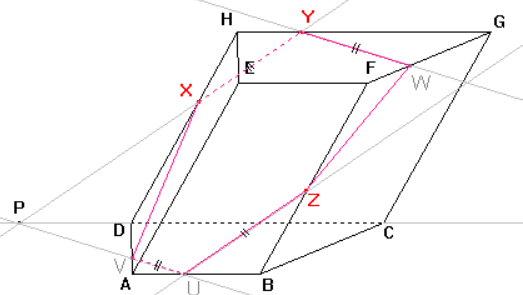
Dle důsledku 1: Body Z, \ W roviny řezu leží v rovině boční stěny, tedy i jejich spojnice leží v rovině této stěny. Průnik spojnice a stěny je další stranou řezu.
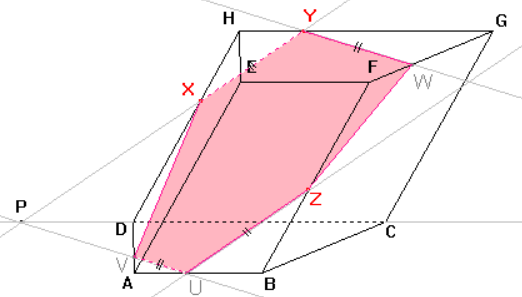
Nyní známe všechny vrcholy a strany mnohoúhelníku, který je řezem daného tělesa.
Příklady, které se mohou objevit v testu: 1), 2), 3), ... doplnit