Mnohočlen je speciálním případem výrazu. Mnohočlenem se rozumí součet konečného počtu členů, které jsou součinem reálné kosntanty a jedné nebo více proměnných s přirozenými exponenty. Například:
Mnohočlen se třemi proměnnými: x^2y+5xy^2-\frac{1}{2}z^2
Mnohočlen se dvěma proměnnými: x^2+xy+\sqrt{2}y
Mnohočlen s jednou proměnnou: x^2+2x+3
Naopak tomu například x^2+2 \sqrt{x}, \frac{2}{3}x+2-\frac{1}{x} nejsou mnohočleny, protože některé proměnné nemají přirozené exponenty.
Definice: Mnohočlen (polynom) n-tého stupně s jednou proměnnou x je výraz:
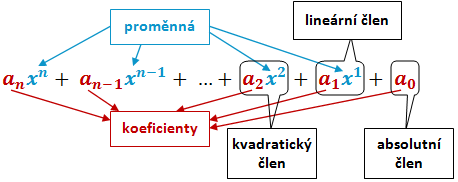
\forall a \in \R, \forall x \in \R, \forall n \in \N: a_nx^n+a_{n-1}x^{n-1}+...+a_2x^2+a_1x+a_0, kde a_n \neq 0
Koeficienty a_0, a_1, ..., a_n se nazývají koeficienty mnohočlenu. Sčítanec a_kx^k se nazývá člen k-tého stupně.
Pro některé členy mnohočlenu (polynomu) máme speciální pojmenování.
- Člen a_0 se nazývá absolutní člen.
- Člen a_1x se nazývá lineární člen.
- Člen a_2x^2 se nazývá kvadratický člen.
Dalším důležitým parametrem je tzv. stupeň polynomu. Stupeň polynomu odpovídá nejvyššímu exponentu proměnné v mnohočlenu. Například mnohočlen 5x^2+3x-1 je mnohočlen druhého stupně, který má tři členy (tři sčítance).
Definice: Mnohočlen (polynom) n-tého stupně s více proměnnými x, y, z, ... je například výraz:
x^5y^3z^4+x^3y^2-2xyz^3
Stupeň polynomu je pak nejvyšší součet u jednotlivých mocnin. Tedy x^5y^3z^4 je člen stupně 5+3+4=12. Člen x^3y^2 je člen stupně 3+2=5. Člen -2xyz je člen stupně 1+1+1=3.
Můžeme tedy říci, že polynom x^5y^3z^4+x^3y^2-2xyz^3 je polynomem dvanáctého stupně.
Sčítání mnohočlenů (polynomů)
Sčítat a odčítat můžeme pouze koeficienty u členů téhož stupně.
(3x^3-2x^2+x)-(4x-3x^2-2x^3)=\\=3x^3-2x^2+x-4x+3x^2+2x^3=\\=5x^3+x^2-3x (2x^2+4x^2y-5xy^2+3y^2)-(4x^2-5xy^2+2x+6)=\\=2x^2+4x^2y-5xy^2+3y^2-4x^2+5xy^2-2x-6=\\=-2x^2+4x^2y+3y^2-2x-6Násobení mnohočlenů (polynomů)
Při násobení mnohočlenu mnohočlenem násobíme každý člen jednoho mnohočlenu s každým členem mnohočlenu druhého.
(2x-3) \cdot (2x-3) + (3x+4) \cdot (3x+4) - (4x-5) \cdot (4x+5)=\\=(4x^2-6x-6x+9)+(9x^2+12x+12x+16)-(16x^2+20x-20x-25)=\\=4x^2-12x+9+9x^2+24x+16-16x^2+25=\\=4x^2+9x^2-16x^2-12x+24x+9+16+25=\\=-3x^2+12x+50
Při počítání s mnohočleny a následně i úpravě výrazů můžeme, pro zrychlení výpočtů, využít následující vzorce:
(a+b) \cdot (a+b) = (a+b)^2 = a^2+2ab+b^2 (a-b) \cdot (a-b) = (a-b)^2 = a^2-2ab+b^2 (a+b) \cdot (a-b) = a^2-b^2 a^3+b^3=(a+b) \cdot (a^2-ab+b^2) a^3-b^3=(a-b) \cdot (a^2+ab+b^2) (a+b)^3=a^3+3a^2b+3ab^2+b^3 (a-b)^3=a^3-3a^2b+3ab^2+b^3Poslední dva zmiňované vzorce není nutné si pamatovat, jelikož je lze rychle odvodit podle následujícího schématu. Načrtneme si trojúhelník, jehož dvě strany jsou složeny pouze z jedniček. Vnitřek trojúhelníku je složen s čísel, které jsou součtem dvou čísel nad. Tento trojúhelník se nazývá Pascalův trojúhelník.

Začněme nejprve vzorcem (a+b)^3=a^3+3a^2b+3ab^2+b^3. Závoraka je umocňena na třetí, proto vezmeme třetí řádek, ve kterém se nachází číselná kombinace 1-3-3-1. Protože je v závorce součet, výsledný rozložený výraz bude obsahovat samá +.
Další věcí, kterou je nutno si uvědomit, jsou exponenty v rozloženém výrazu u proměnných a, b. Závorka je umocněna na třetí, pak tedy začneme a^3b^0. Protože cokoliv umocněno na nultou je jedna, pak tedy a^3.
U dalšího čísla postupně snižujeme exponent u proměnné a a naopak zvyšujeme u proměnné b. Podívejme se na třetí řádek trojúhelníku a vidíme číselnou kombinaci 1-3-3-1. Této kombinaci budou odpovídat členy a^3b^0 - a^2b^1 - a^1b^2 - a^0b^3. Pak tedy:
(a^3+b^3)^3=1a^3b^0 + 3a^2b^1 + 3a^1b^2 + 1a^0b^3=\\=a^3+3a^2b+3ab^2+b^3Podívějme se, pokud bychom měli výraz (a+b)^5. Podíváme se do Pascalova trojúhelníku a vidíme číselnou kombinaci 1-5-10-10-5-1. V závorce je +, pak tedy i ve výsledném výrazu bude všude +. Exponenty u proměnné a postupně snižujeme z čísla 5. U proměnné b naopak jdeme z 0 do čísla 5
(a+b)^5=1a^5b^0+5a^4b^1+10a^3b^2+10a^2b^3+5a^1b^4+1a^0b^5=\\=a^5+5a^4b+10a^3b^2+10a^2b^3+5ab^4+b^5Jak by to bylo, pokud bychom měli vzorec s rozdílem, tedy
(a-b)^3=a^3-3a^2b+3ab^2-b^3Postup je úplně stejný jako v předchozích příkladech, kdy se v závorce objevil součet. Jediným rozdílem je pouze změna znamének ve finálním výrazu. Tato změna je provedena tak, že každé druhé plus v předchozích příkladech nahradíme mínusem, tedy namísto kombinace + + + + budeme mít kombinaci + - + - . Porovnejme:
(a+b)^3=a^3+3a^2b+3ab^2+b^3 (a-b)^3=a^3-3a^2b+3ab^2-b^3 (a+b)^5=a^5+5a^4b+10a^3b^2+10a^2b^3+5ab^4+b^5 (a-b)^5=a^5-5a^4b+10a^3b^2-10a^2b^3+5ab^4-b^5!!!Pozor, tento postup neplatí pro vzorce a^3+b^3, a^3-b^3, a^4+b^4, a^4-b^4, atd. V tomto případě nejsme schopni nalézt podobné univerzální řešení a je nutné využít tabulky.
Dělení polynomu polynomem
Při dělení polynomu polynomem (mnohočlenu mnohočlenem) si nejprve seřadíme všechny členy v obou polynomech od členů s nejvyšším exponentem po nejnižší (usnadníme si tím práci). Následně dělíme vždy nejvyšší člen dělence nejvyšším členem dělitele. Členem, který vyjde, vynásobíme celého dělitele a výsledný mnohočlen odečteme od dělence. Tím získáme nový mnohočlen nižšího stupně.
Pokud není nově vzniklý mnohočlen nižšího stupně než dělitel, tento proces opakujeme.
Pokud nám vyjde nenulový zbytek, zapisujeme ho do výsledku ve tvaru zlomku, kde v čitateli je zybtek a ve jmenovateli dělitel původního zadání.

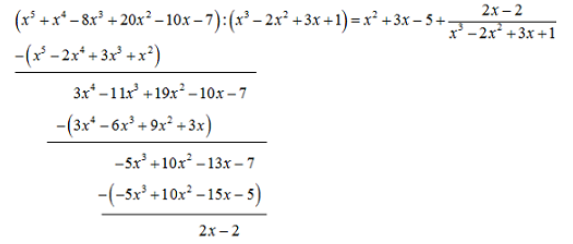
Rozklad mnohočlenů (polynomů)
Rozložit mnohočlrn znamená vyjádřit ho jako součin mnohočlenů nižšího stupně. Lze to provést několika způsoby (vytýkání, pomocí vzorců, ...)
Vytýkání
xy-2y+xz-2z=y \cdot (x-2) + z \cdot (x-2)=\\=(x-2) \cdot (y+z)Pomocí vzorců
4x^2-8xy+y^2+4xy=4x^2-4xy+y^2=\\=(2x-y)^2=(2x-y) \cdot (2x-y)V tomto příkladu jsme využili vzorec a^2+2ab+b^2=(a-b)^2
(2x+y)^2-(x-2y)^2=\\=[(2x+y) - (y-2y)] \cdot [(2x+y) + (y-2y)]=\\=[2x+y-y+2y] \cdot [2x+y+y-2y]=\\=(x+3y) \cdot (3x-y)V tomto případě jsme využili vzorce a^2-b^2=(a-b) \cdot (a+b)
Příklady (opakování učiva základní školy - příklady pro 8. ročník ZŠ) - stupeň polynomu, sčítání/odčítání/ násobení polynomu, rozklad vytýkáním a pomocí vzorců
Příklady - Pascalův trojúhelník (rozklad mnohočlenů pomocí vzorců), dělení mnohočlenu mnohočlenem
Pro příklady využijte www.wolframalpha.com, ve kterém si vymyslíte vlastní příklad, který si vyzkoušíte vypočítat bez použití počítače.
V případě dělení polynomu polynomem dosazujte za dělitele "hezké" výrazy, například (x+3). Zejména pak první člen, pokud by nebyl například x ale 3x, pak byste dostali ve výsledku zlomky, které by při dalších krocích přinášeli složitější výpočet.
V případě, že u dělení polynomu polynomem nevidíte výsledek v sekci Alternate forms ve tvaru, kter7 požadujete, klikněte u Alternate forms na More. Následně dostanete výraz, který požadujete. Nedivte se také tomu, že wolfram řadí sčítance dle mocnin. Vizuálně můžete dostat jiný tvar, ale při sčítání platí a+b+c=a+c+b=b+a+c=....
Někdy je také možné, že vyjde dělení bezezbytku. Pak člen v podílovém tvaru bude roven nule. Výsledek ale ve wolframu naleznete.
Příklady: Sbírka úloh z matematiky pro SOŠ a studijní obory SOU. 3. vyd. Praha: SPN, 1989. Učebnice pro střední školy. ISBN 80-04-24148-4.
Příklady: HUDCOVÁ, Milada a Libuše KUBIČÍKOVÁ. Sbírka úloh z matematiky pro SOŠ, SOU a nástavbové studium. 2. vyd. Praha: Prometheus, 2005. ISBN 978-80-7196-318-9.