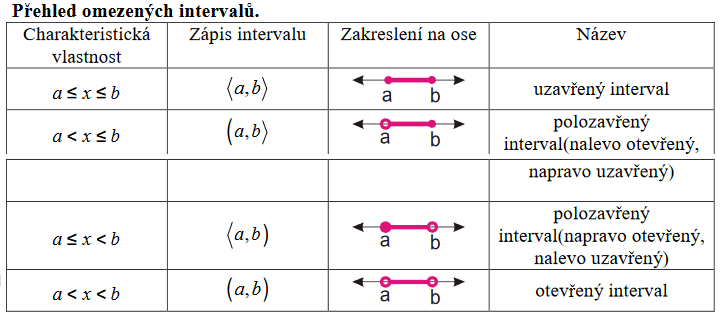
Intervaly se v matematice hojně používají a jsou obsaženy v kdejaké definici. Interval je množina bodů, která se ohraničena dvěma krajními body. Dále rozlišujeme otevřené a uzavřené intervaly.
Následují příklady ukazují varianty intervalů (všechny v množině reálných čísel, není-li řečeno jinak):
Uzavřený interval od jedné do dvou. Do intervalu spadají všechna reálná čísla mezi jedničkou a dvojkou včetně jedničky a dvojky:
\langle 1;2 \rangle
Otevřený interval od jedné do dvou. Do intervalu spadají všechna reálná čísla mezi jedničkou a dvojkou, ale samotná čísla jedna a dva tam nepatří.
(1;2)
Interval je zleva uzavřený a zprava otevřený. Do intervalu spadají všechna čísla mezi nulou a jedničkou, včetně nuly samotné, ale jednička do intervalu nepatří. Lze také říci, že interval je polouzavřený zleva nebo polootevřený zprava.
\langle 0;1)
Interval je zleva otevřený a zprava uzavřený. Do intervalu spadají všechny čísla mezi čísly p a q, včetně čísla q, ale vyjma čísla p. Lze také říci, že interval je polouzavřený zprava nebo polootevřený zleva.
(p;q \rangle
Zleva uzavřený interval a zprava otevřený. Pokud máte v intervalu nekonečno, používejte z dané strany otevřený interval, nekonečno nemá nějaký krajní konečný bod, uzavřený interval tam nemá smysl. Interval je polouzavřený zleva.
\langle 0; \infty )
Zde následuje změna, nepracujeme s množinou reálných čísel, ale s množinou reálných čísel. Máme z obou stran uzavřený interval a v daném intervalu je tak celkem pět čísel: 1, 2, 3, 4 a 5.
\langle 1;5 \rangle \subset \N
Stejný případ jako před chvílí, pouze je interval zleva otevřený a tak jednička nepatří do intervalu a výčet všech prvků intervalu je: 2, 3, 4 a 5.
(1;5 \rangle \subset \N
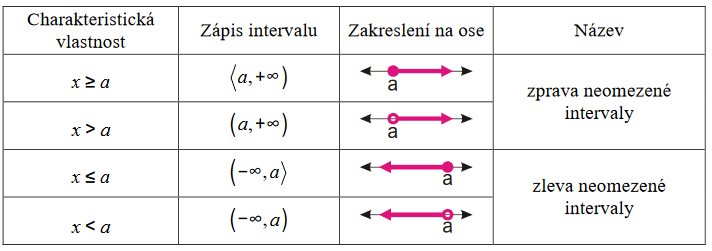
Gometrická interpretace
Intervaly obyčejně zobrazujeme na číselné ose jako úsečky, krajní body volíme podle toho, zda je interval uzavřený nebo otevřený. Pokud je interval uzavřený, bude kolečko zobrazující bod vybarvené, pokud je otevřený, bude nevybarvené, bude to jen obrys, jen kružnice.
Následující obrázek zachycuje zobrazení třech intervalů vždy od dvou do šesti, ale liší se v uzavřenosti stran. Takže popořadě budou zobrazeny tyto intervaly:
\langle 2;6 \rangle
(2;6 \rangle
(2;6)

Interval jako množina
Jak je vidět, interval není nic jiného než podmnožina množiny, nad kterou je definován. Proto můžeme s intervaly pracovat jako s množinami provádět s nimi množinové operace. Například sjednocení by mohlo vypadat takto:
\langle 0;5 \rangle \cup \langle 5;10 \rangle = \langle 0;10 \rangle
Pozor na otevřené intervaly, tam by ta rovnost totiž neplatila, protože pětka do výsledného intervalu nepatří:
(0;5) \cup (5;10) \ne (0;10)
Správně by to mohlo vypadat například takto:
(0;5) \cup (5;10) = (0;10) -\{5\}
Příklady:
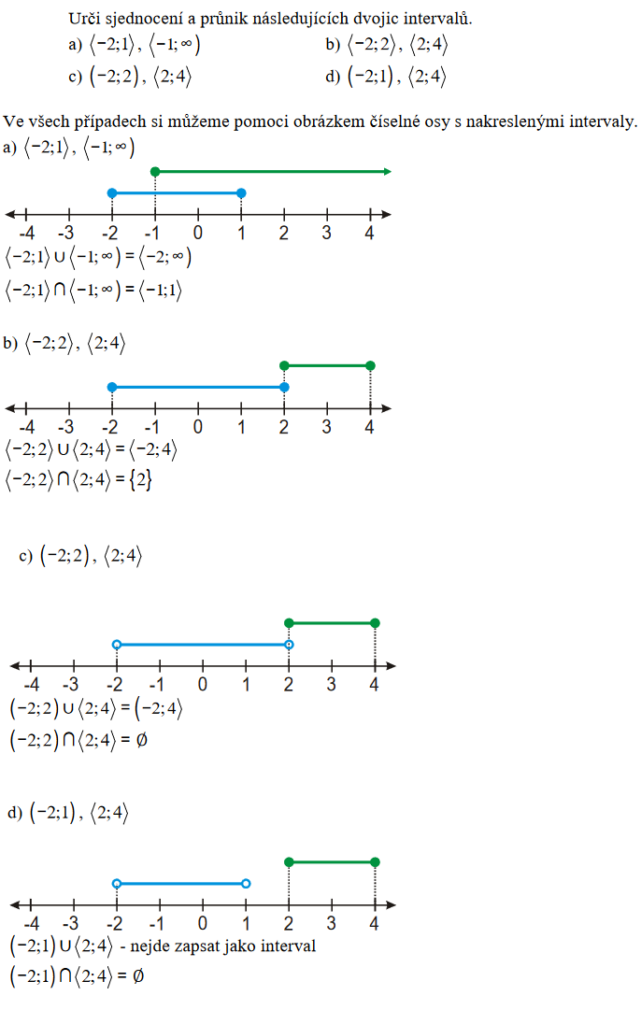
Příklady k procvičení: Vypočtěte příklady 24.1, 24.12 - 24.17, 24.19 - 24.20, 24.25 (c, d, e, f, g)
KRIEGELSTEIN, Eduard. Sbírka úloh z matematiky pro střední průmyslové školy a střední zemědělské technické školy. 10. vyd. Praha: Státní pedagogické nakladatelství, 1965.