Sinus úhlu \alpha se rovná poměru délky přilehlé odvěsny ku délce přepony. Co to znamená? Pokud spočítáme (na kalkulačce například) cosinus úhlu \alpha, získáme hodnotu podílu
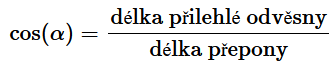
Zkusíme si to na tomto trojúhelníku a úhlu \beta.

Délky stran jsou: a=5, b=3, c=4. Přilehlá odvěsna k úhlu \beta je strana c, přepona je strana a. Vypočítáme podíl \frac{c}{a}, tedy \frac{4}{5} , což je 0,8. Cosinus úhlu \beta se tak rovná 0,8. Úhel \beta má velikost 36,87°.
Poznámka: Do kalkulačky vložte cos^{-1}(0,8) a získáte výsledek 36,87°, po přepnutí na stupně a minuty dostanete hodnotu 36° 52´.
Pokud tento úhel naskládáte do kalkulačky a vypočítáte cosinus, získáte právě 0,8 (po drobném zaokrouhlení).
K čemu je to dobré?
Je to dobré v případě, kdy znáte jeden úhel a délku jedné strany a potřebujete dopočítat zbývající strany.
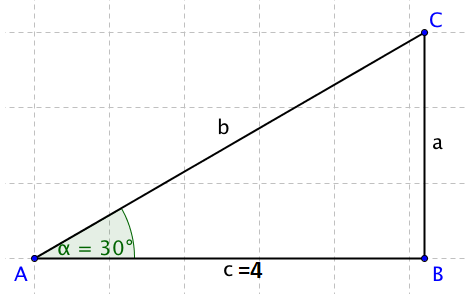
Jako první si napíšeme, co vlastně víme. Známe úhel \alpha . Víme, že cosinus tohoto úhlu je rovný poměru přilehlé odvěsně (což je strana c) ku přeponě (strana b). Zapsáno matematicky:
sin(\alpha) = \frac{c}{b}
Sinus úhlu známe, respektive můžeme vypočítat, délku strany c známe. Jediné, co neznáme, je délka strany b. Tuto proměnnou se tak budeme snažit osamostatnit. Jako první vynásobíme rovnici délkou strany b. Dostaneme
b \cdot cos(\alpha) = c
a teď už jen rovnici vydělíme cos(\alpha) a dostáváme požadovaný tvar s délkou strany b na levé straně:
b= \frac{c}{cos(\alpha)}
Délku strany c známe, ta je rovna 4. Cosinus 30° je roven 0,87. Dosadíme:
b = \frac{3}{0,87}=3,45
Strana b má délku 3,45.
Vzorový příklad - známe délky stran, vypočítáme vnitřní úhly:
Pravoúhlý trojúhelník má délky stran a=6 cm, b=10 cm, c=8 cm. Vypočtěte velikosti vnitřních úhlů využitím funkce cosinus.
Tento trojúhelník je pravoúhlým. Ověření by bylo možné provést na základě platnosti Pythagorovy věty. Přeponou je nejdelší strana, tedy strana b.
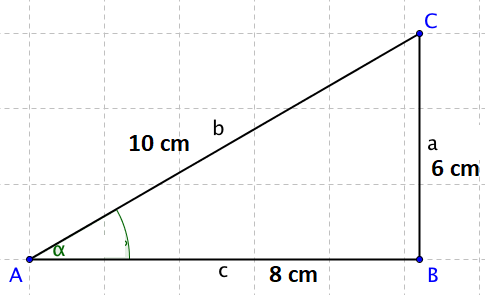
cos(\alpha) = \frac{c}{b}
cos(\alpha) = \frac{8}{10}
cos(\alpha) = 0,8
Nyní musíme na kalkulačce zmáčknout klávesu cos^{-1} a zadat hodnotu 0,8. Většinou je tato klávesa umístěta jako klávesa cos, jen je nutné před jejím zmáčknutím zmáčknout klávesu shift.
cos^{-1}(0,8)=0,644
Nyní na kalkulačce zmáčkneme symbol pro převod desetinného čísla na stupně a minuty, většinou vypadá takto: °´´. Dostáváme pak:
cos^{-1}(0,8)=36,87°
Zápsáno ve wolframalpha: https://www.wolframalpha.com/input/?i=arccos%280.8%29
Jelikož je trojúhelník pravoúhlý, můžeme říci, že \beta = 90°. Dále pak víme, že součet vnitřních úhlu v trojúhelníku je 180°. Úhel \gamma je pak tedy roven:
\gamma = 180° - 90° - 36,87° = 63,13°
Příklady:
- V pravoúhlém trojúhelníku je úhel proti kratší odvěsně
30°. Vypočítej délku delší odvěsny, je-li přepona 8 cm. [b = 4 \sqrt{3} ]
- V pravoúhlém trojúhelníku je úhel proti kratší odvěsně
60°. Vypočítej délku přepony, je-li delší odvěsna 8 cm . [c = 16 cm ]
V pravoúhlém trojúhelníku je délka odvěsny 50 cm,
přepony 100 cm . Vypočítej velikost úhlu podél zadané
odvěsny. [\alpha = 60° ]