Obor (množina) přirozených čísel
Přirozená čísla dokážeme jmenovat, zapisovat číslicemi a znázorňovat na číselné ose. Rozlišujeme významy slov číslice (cifra) a číslo. Číslice (cifra) je grafický symbol znázorňující číslo. Například číslo 425 se skládá z třech číslic (cifer), a to z čtyřky, dvojky pětky.
Definice přirozených čísel: Přirozená čísla jsou čísla 1, 2, 3, ... Pozor, nula nepatří mezi přirozená čísla!
Značení:
\N obor (množina) přirozených čísel
\N_0 množina přirozených čísel včetně nuly
Obor (množina) celých čísel
V oboru přirozených čísel byl problém rozdíl některých přirozených čísel, jako například rozdíl čísel 4-8=8. Číslo -4 ale nespadá do oboru přirozených čísel.
Definice celých čísel: Celá čísla jsou čísla ..., -3, -2, -1, 0, 1, 2, 3, ...
Značení:
\Z obor (množina) celých čísel: ..., -3, -2, -1, 0, 1, 2, 3, ...
\Z_0^+ množina kladných celých čísel včetně nuly: 0, 1, 2, 3, ...
\Z_0^- množina záporných celých čísel včetně nuly: ..., -3, -2, -1, 0
\Z^+ množina kladných celých čísel: 1, 2, 3, ...
\Z^- množina záporných celých čísel: ..., -3, -2, -1
Obor (množina) racionálních čísel
Množina racionálních čísel Q obsahuje právě ta čísla, jež lze vyjádřit ve tvaru \frac{p}{q} , kde p je celé číslo a q je přirozené číslo. Tento zápis však není jednoznačný. Každé racionální číslo lze vyjádřit nekonečně mnoha způsoby krácením či rozšiřováním daného zlomku. Mezi všemi těmito vyjádřeními existuje jediné, které má tu vlastnost, že čísla p, q jsou nesoudělná, tj. jejich společný dělitel je pouze číslo jedna. O takovém zlomku říkáme, že je vyjádřením daného racionálního čísla vzákladním tvaru. Například zlomek \frac{2}{3} lze vyjádřit jako: \frac{4}{6}, \frac{20}{30}, \frac{-2}{-3}, \frac {-6}{-9},... .
Slovo racionální se zde používá ve významu podílový, poměrový. Nikoli tedy ve filosofickém významu rozumový. Každé přirozené i celé číslo je číslem racionálním. Lze je totiž vyjádřit ve tvaru zlomku, jehož jmenovatel je roven 1.
3 = \frac{3}{1}; 0 = \frac{0}{1}; −23 = \frac{−23}{1}.
Značení:
Q obor (množina) racionálních čísel
Q_0^+ obor (množina) kladných racionálních čísel včetně nuly
Q_0^- obor (množina) záporných racionálních čísel včetně nuly
Q^+ obor (množina) kladných racionálních čísel
Q^- obor (množina) záporných racionálních čísel
Početní operace s racionálními čísly:
\frac{p}{q} + \frac{r}{s} = \frac{ps+qr}{qs}
\frac{p}{q} - \frac{r}{s} = \frac{ps-qr}{qs}
\frac{p}{q} \cdot \frac{r}{s} = \frac{p \cdot r}{q \cdot s}
\frac{p}{q} : \frac{r}{s} = \frac{p}{q} \cdot \frac{s}{r} = \frac{p \cdot s}{q \cdot r}
Racionální čísla tedy můžeme zapsat ve tvaru:
- Zlomku
- Desetinného čísla
- Nekonečného periodického desetinného rozvoje s vyznačenou periodou
- Desetinným číslem sukončeným rozvojem
Pozor!!! Racionální čísla nemohou mít nekonečný neperiodický rozvoj. Takováto čísla se nazývají iracionální!!!

Každé číslo ale nelze rozložit tak, aby se ve jmenovateli objevily násobky 10!


Vobou případech můžeme vdělení pokračovat libovolně dlouho, zbytek je stále nenulové číslo, protože v desetinném rozvoji se opakuje stále stejná skupina číslic. Tato skupina číslic se nazývá perioda. Při zápise čísla vyznačíme nad periodu pruh a tyto číslice dále nepíšeme.
\frac{10}{33} = 0,\overline{30}
\frac{15}{22} = 0,6\overline{81}
Periodou je u prvního příkladu skupina číslic 30, v druhém čísle skupina číslic 81. V nekonečném desetinném rozvoji se může před periodou vyskytnout skupina číslic, která se neopakuje. Takovýto rozvoj se nazývá neryze periodický a skupina neopakujících se číslic se nazývá předperioda. Rozvoj, v němž se předperioda nevyskytuje, se nazývá ryze periodický.
0.6\overline{81} je příkladem neryze periodického rozvoje, kde číslice 6 je předperioda. Naopak číslo 0,\overline{30} je číslem ryze periodickým.




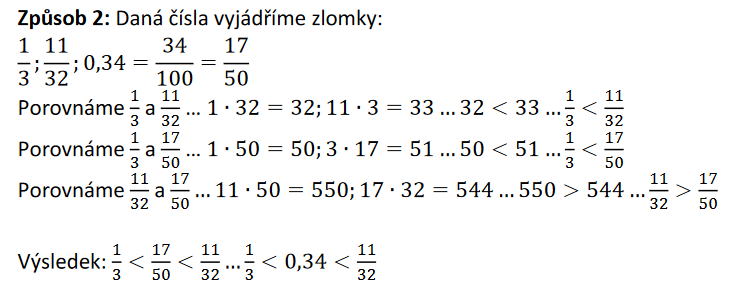
Smíšené číslo
Některá racionální čísla můžeme zapsat jako čísla smíšená. Například číslo \frac{29}{13}, které je zapsáno v základním tvaru, lze zapsat jako smíšené číslo 2 \frac{3}{13}. Čteme dvě a tři třináctiny, nikoli dva krát tři třináctiny!!!
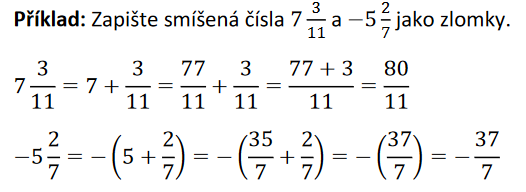
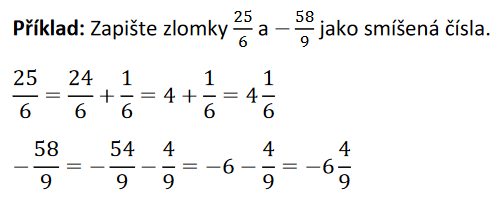
Znázorňování racionálních čísel na číselnou osu
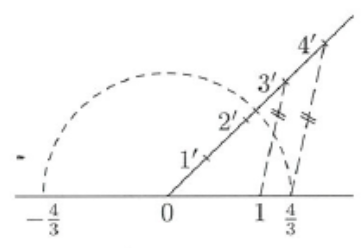
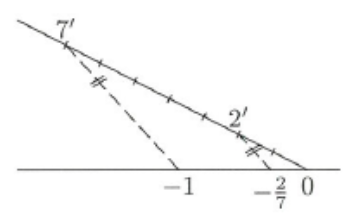
Příklady:
KUBÁT, Josef, Josef PILGR a Dag HRUBÝ. Sbírka úloh z matematiky pro střední školy: maturitní minimum. Praha: Prometheus, 1996. Učebnice pro střední školy (Prometheus). ISBN 80-7196-030-6.
BUŠEK, Ivan a Emil CALDA. Matematika pro gymnázia. 4. vydání. Praha: Prometheus, 2008. Učebnice pro střední školy (Prometheus). ISBN 978-80-7196-366-0.
KRIEGELSTEIN, Eduard. Sbírka úloh z matematiky pro střední průmyslové školy a střední zemědělské technické školy. Praha: Státní pedagogické nakladatelství, 1965. Pomocné knihy pro žáky (Státní pedagogické nakladatelství).
POLÁK, Josef. Středoškolská matematika v úlohách. 2., upr. vyd. Praha: Prometheus, 2011. ISBN 80-7196-337-2.