Dynamika studuje příčiny pohybu těles a příčiny změn jejich pohybového stavu. Na rozdíl od kinematiky, která zkoumá, jak se tělesa pohybují, dynamika se zabývá otázkami, přoč a za jakých podmínek se tělesa pohybují. V dalším výkladu budeme považovat tělesa za hmotné body.
Síla jako fyzikální veličina
Síla je fyzikální veličina, která charakterizuje vzájemné působení těles. Vzájemné působení těles neboli interakce se projevuje:
- Při vzájemném dotyku těles (přemisťování těles rukou, při nárazu míče na stěnu, při výstřelu náboje z pušky).
- Prostřednictvím silových polí, přičemž nemusí dojít k bezprostřednímu dotyku těles (prostřednictvím gravitačního pole se přitahují Země a Měsíc, Slunce a planety).
Dle původu interakce nebo podle objektů, které na sebe působí, jsou mnohé síly pojmenovány:
- tlaková
- třecí
- hydrostatická
- gravitační
- elektrická
- magnetická
Společnou vlastností všech interakcí je, že síly jsou vždy vyvolány vzájemným působením hmotných objektů. Neexistuje síla sama o sobě.
Síla F je vektorová fyzikální veličina, která je určena velikostí, směrem a polohou svého působiště.
Hlavní jednotkou síly je Newton (N). Síla F se znázorňuje podobně jako jiné vektorové veličiny orientovanou úsečkou, jejíž délka vyjadřuje velikost síly, její poloha s vyznačenou šipkou směr síly a počáteční bod vektoru působiště síly. Na následujícím obrázku je znázorněna síla F o velikosti 4 N. Působiště síly je v bodě P. Působiště síly je většinou do těžiště tělesa. Pokud nahradíme těleso hmotným bodem, je působiště v tomto bodě.
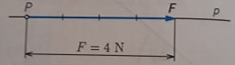
Skládání sil
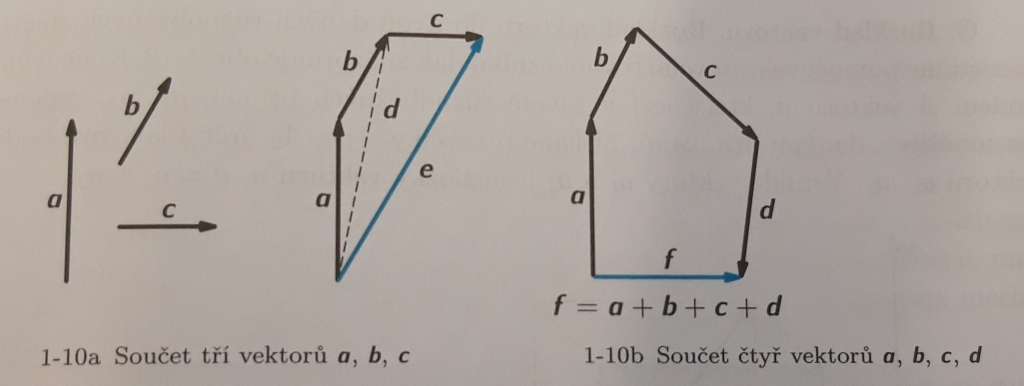
Působí-li na hmotný bod nebo těleso v jednom jeho bodě současně několik sil 
, můžeme je nahradit jedinou silou F, která má stejný pohybový účinek jako dané síly. Postup, kterým toto nahrazování sil provádíme, se nazývá vektorové skládání sil.
Síly , které skládáme, nazýváme složky. Výslednou silou F, která je nahrazuje, výslednice. Výslednice se rovná vektorovému součtu složek, tedy
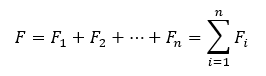
Čtyři nejjednodušší příklady skládání dvou sil působící v jednom bodě jsou uvedeny v následující tabulce.
Příklady k procvičení zde.
Izolované těleso
Tělese, na které nepůsobí silou žádné jiné těleso, a to ani při dotyku ani prostřednictvím pole, nazýváme izolované těleso. Můžeme-li těleso nahradit hmotným bodem, jde o izolovaný bod.
Pokud je izolované těleso v dané vztažné soustavě v klidu, zůstane v klidu. To znamená, že žádné těleso se nedá do pohybu samo od sebe, tj. bez působení jiného tělesa.
V pozemských podmínkách, kde se každé těleso nachází v tíhovém poli Země, však izolovaná tělesa ve skutečnosti neexistují. Proto zavádíme pojem model izolovaného tělesa.
Modelem izolovaného tělesa je těleso, na které sice působí silami jiná tělesa, ale výslednice těchto sil je nulová (nehybná kulička na vodorovné desce stolu - tíhová síla, kterou působí Země na kuličku, se ruší stejně velkou silou opačného směru, kterou působí na kuličku deska stolu.
Pokud je izolované těleso v pohybu, zůstává dále v pohybu (předpokládejme dokonale hladkou podložku bez odporu prostředí, ...).
První Newtonův zákon
Každé těleso setrvává v klidu nebo rovnoměrném přímočarém pohybu, pokud není nuceno silovým působením jiných těles svůj pohybový stav změnit.
Ze zákona vyplývá, že v klidu nebo rovnoměrném přímočarém pohybu setrvá každé izolované těleso (izolovaný bod). Pro izolované těleso jsou klid nebo rovnoměrný přímočarý pohyb dva rovnocenné pohybové stavy, pro jejichž rychlost platí v = konst., tedy i v = 0, a pro zrychlení a = 0. Jsou to stavy s nulovým zrychlením.
První pohybový zákon ukazuje důležitou vlastnost všech těles, na jejich setrvačnost. Setrvačnost těles v klidu se projevuje, chceme-li je uvést do pohybu, setrvačnost těles v pohybu, chceme-li změnit směr nebo vylikost jejich rychlosti. Proto první Newtonův zákon označujeme také jako zákon setrvačnosti.
Inerciální vztažná soustava
Vztažná soustava, ve které izolované těleso (izolovaný hmotný bod) setrvává v klidu nebo ovnoměrném přímočarém pohybu, se nazývá inerciální vztažná soustava. V inerciální vztažné soustavě platí zákon setrvačnosti. V inerciální vztažné soustavě může být těleso uvedeno z klidu do pohybu nebo naopak, či jakkoliv změněn jeho pohybový stav, jen silovým působením jiných těles.
Příklady inerciální vztažné soustavy: vlak jede konstantní rychlostí a rovně. Míček je umístěn na podlaze a je vůči vlaku v klidu.
Vztažná soustava, ve které těleso nezůstává v klidu nebo rovnoměrném přímočarém pohybu se nazývá neinerciální vztažná soustava. V neinerciální vztažné soustavě dochází ke změně pohybového stavu tělesa bez silového působení jiných těles. Zákon setrvačnosti zde neplatí.
Příklady neinerciální vztažné soustavy: míček leží nehybně na podlaze vlaku, který stojí nebo jede rovně konstantní rychlostí. Pokud vlak změní rychlost nebo zahne, míček se pohne a nesetrvává ve svém původním stavu.
Každá vztažná soustava, která je vzhledem k dané inerciální soustavě v klidu nebo rovnoměrném přímočarém pohybu, je rovněž inerciální.
Nejčastěji volíme inerciální vztažnou soustavu povrch Země, pak každá soustava, která je vzhledem k povrchu Země v klidu nebo rovnoměrném přímočarém pohybu, je rovněž inerciální.
Galileův princip relativity: Všechny inerciální soustavy jsou pro popis mechanických dějů rovnocené. Ve všech inerciálních vztažnýc soustavách platí stejné zákony a rovnice, které je vyjadřují, mají stejný tvar.
Druhý Newtonův zákon
Izolované těleso v inerciální vztažné soustavě setrvává v klidu nebo rovnoměrném přímočarém pohybu. Pokud ale začnou na těleso působit silami jiná tělesa, jejich výslednice se nebude rovnat nule a dojde ke změně pohybového stavu. Změní se rychlost tělesa a těleso se začne pohybovat se zrychlením.
Druhý pohybový zákon vyjadřuje vztah mezi výslednicí sil F působících na těleso a zrychlením a tělesa.
Pokud budeme působit větší silou na těleso, dosáhneme většího zrychlení. Pokud bude mít ale těleso větší hmotnost, pak zrychlení bude menší. Odtud dostáváme tvar Druhého Newtonowa zákona:
Velikost zrychlení a je přímo úměrné působící síle F a nepřímo úměrná hmotnosti m tělesa.
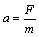
Směr zrychlení 
je shodný se směrem výslednice sil 
, tedy vektorově zapsáno:
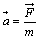
Vyjádříme-li ze zvorce sílu F, pak jednotkou bude Newton (N), pro kterou platí: 1 N = kg·m·s-2
Síla o velikosti 1 N uděluje tělesu o hmotnosti 1 kg zrychlení 1 m·s-2.
Druhý pohybový zákon umožňuje dynamické měření hmotnosti tělesa, tj. měření hmotnosti tělesa na základě pohybových účinků síly na těleso. Tato metoda má význam tehdy, není-li možné určit hmotnost tělesa vážením (elementární částice, hvězdy). Tato hmotnost se nazývá setrvačná hmotnost a charakterizuje setrvačné vlastnosti těles.
Tíha a tíhová síla
Z druhého pohybového zákona vyplývá, že na těleso, které se pohybuje se stlým zrychlením, působí stálá výsledná síla. Příkladem pohybu se stálým zrychlením je volný pád. Zrychlení volného pádu se nazývá tíhové zrychlení.
Tíhové zrychlení g uděleju tělesům v blízkosti povrchu Země tíhová síla 
, kterou jsou všechna tělesa přitahována k Zemi.
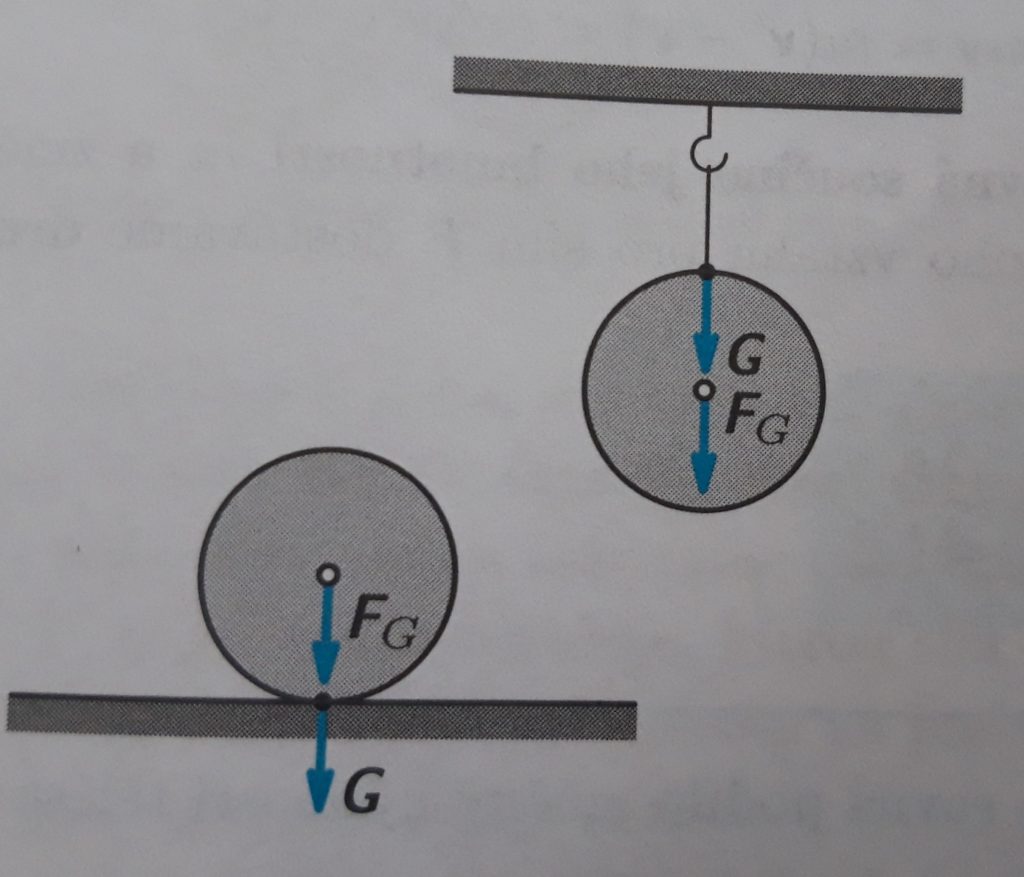
Tíhová síla má stejný směr jako tíhové zrychlení g. Od tíhové síly odlišujeme veličinu tíha G. Tíha se projvuje jako tlaková síla, kterou působí těleso na nehybnou vodorovnou podložku, nebo jako tahová síla, kterou působí těleso na nehybný svislý závěr. Tíha tělesa vzniká vždy jako důsledek tíhové síly, kterou působí Země na těleso.
Tíhová síla a tíha se také liší polohou svých působišť. Působiště tíhové síly klademe do těžiště tělesa, působiště tíhy G je ve stykové ploše tělesa s podložkou nebo v bodě závěsu. Přitom však na daném místě povrchu Země mají tíhová síla i tíha stejný směr i velikost.
Hybnost tělesa
V kinematice se vyjadřuje pohybový stav těles jejich rychlostí. V dynamice zavedl Newton k vyjádření pohybovéhu stavu tělesa veličinu hybnost tělesa.
Hybnost p tělesa je vektor, definovaný jako součin hmotnosti m a okamžité rychlosti tělesa v, tedy
Ze vzorce pro hybnost vyplívá, že jednotkou hybnosti je kilogram metr za sekundu, tedy kg·m·s-1. Je to hybnost tělesa o hmotnosti 1 kg pohybující se rychlostí 1 m·s-1.
V kinematice je zrychlení hmotného bodu definováno jako podíl změny rychlosti a doby, za kterou tato změna nastala, tedy
....................
Dosadíme-li toto zrychlen do druhého pohybového zákona F=ma, dostaneme
...................
Působí li na těleso síla F po dobu ___, změní se jeho rychlost z hodnoty v na hodnotu v´, a tím i jeho hybnost z hodnoty p na hodnotu p´. Změna hybnosti tělesa je pak
Změna hybnosti tělesa ___ se tedy rovná součinu jeho hmotnosti m a změny rychlosti ___. Po dosazení do předchozího vztahu pro sílu F dostáváme druhý pohybový zákon ve tvaru
......................
Výsledná síla působící na těleso se rovná podílu změny hybnosti tělesa a doby, po kterou síla působila.
Velice často se používá upravený tvar, kde časová změna hybnosti tělesa je rovna výslednicí sil, které na těleso působí. Jde o tzv. impuls síly, což je vektor, jehož jednotkou je newton sekunda Ns.
........................
Impuls síly vyjadřuje časový účinek síly na těleso. Jeho velikost závisí jednak na velikost působící síly, jednak na době, po kterou působí síla. Na impulzu síly pak závisí změna hybnosti.