Úvod ke stereometrii, základní pojmy
Mezi základní geometrické pojmy patří bod, přímka a rovina. V předchozích ročnících jsme popsali jejich označení písmeny a připomněli, že každá přímka a každá rovina obsahuje nekonečně mnoho bodů, jsou to tedy příklady nekonečných bodových množin.
V planimetrii jsme se zabývali pouze rovinnými geometrickými útvary, tj. geometrickými ptvary, které jsou částí roviny. Nyní se budeme zabývat prostorovými geoetrickými útvary, tj. geometrickými útvary, které nelze umístit do roviny.
V prostoru pro vzájemnou incidenci bodů (incidence = ležet na / protínat se), přímek a rovin platí následující jednoduché věty:
Věta 1: Dvěma různými body A, \ B prochází právě jedna přímka p je určena body A, \ B, a píšeme p= \leftrightarrow AB nebo p= \leftrightarrow BA.
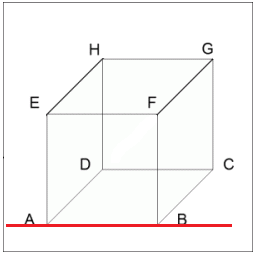
Věta 2: Leží-li dva různé body A, \ B v rovině \varrho, leží i přímka jimi určená v rovině \varrho.
A \in \varrho \wedge B \in \varrho \Rightarrow \ \leftrightarrow p = AB \subset \varrho
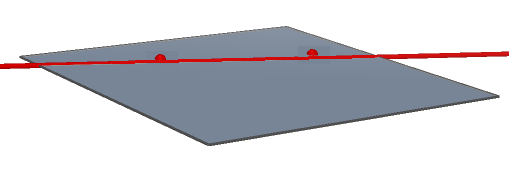
Věta 3: Danou přímkou p a daným bodem X ležící mimo ni prochází právě jedna rovina \varrho.
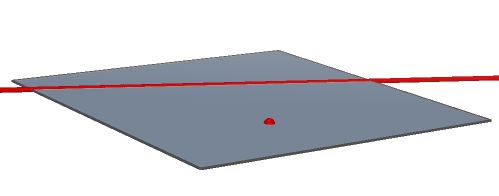
Věta 4: Třemi danými body A, \ B, \ C, které neleží v přímce, prochází právě jedna rovina \varrho.
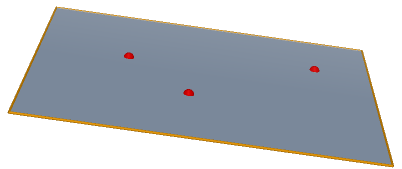
Věta 5: Dvěma různými přímkami p, \ q, které mají společný bod, prochází právě jedna rovina \varrho.
V případech uvedených ve větách 3, 4 a 5 říkáme, že rovina \varrho je určena danými body či přímkami, a píšeme \varrho = \leftrightarrow pX, \ \varrho = \leftrightarrow ABC, \ \varrho = \leftrightarrow pq
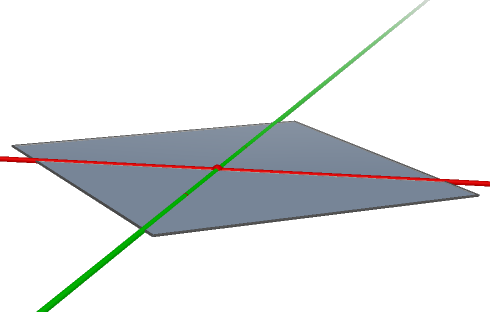
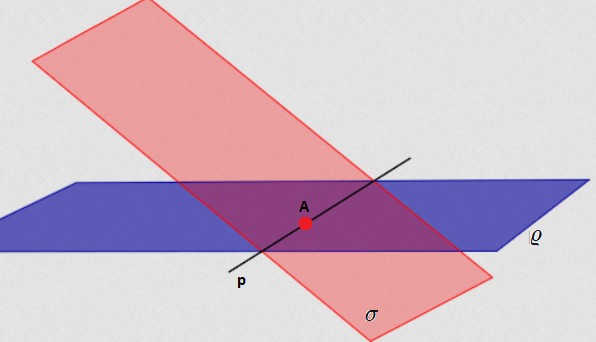
Věta 6: Procházejí-li dvě různé roviny \varrho, \ \sigma týmž bodem A, obsahují právě jednu přímku p, která prochází bodem A. Mimo tuto přímku p nemají už žádný společný bod.
Věta 7: Rovina je jednoznačně určena:
- přímkou a bodem, který na ní neleží;
- dvěma různými rovnoběžkami;
- dvěma různými různoběžkami;
- třemi různými body, které neleží na přímce;
Základní pojmy a značení

Vzájemná poloha přímek v prostoru
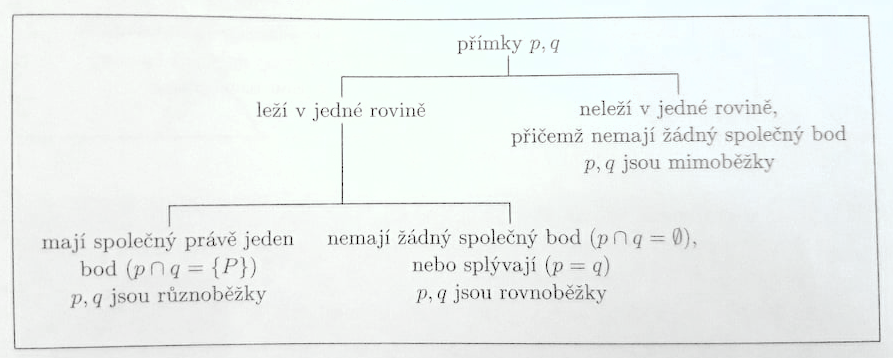
Každé dvě přímky v rovině jsou buď různoběžky, nebo rovnoběžky. V prostoru jsou tři možnosti vzájemné polohy dvojice přímek: Dvě různé přímky p, \ q, které mají právě jeden společný bod P, leží (podlě věty V. 5) v téže rovině; takové přímky se nazývají různoběžné přímky (různoběžky). Bodu P se říká průsečík různoběžek; píšeme P \cap q = \{ P \}.

Dvě různé přímky p, \ q v prostoru, které leží v jedné rovině a nemají žádný společný bod, se nazývají rovnoběžné přímky (rovnoběžky).

V případě splývajících (totožných) přímek v prostoru p=q považujeme přímky za rovnoběžky. Rovnoběžky zapisujeme p \parallel q .
Z věty V. 4 plyne, že dvěma různými rovnoběžkami p, \ q prochází právě jedna rovina \varrho; je jimi tedy určena \varrho = \leftrightarrow pq.
Dvě různé přímky p, \ q v prostoru, které nemají žádný společný bod a neleží v jedné rovině, se nazývají mimoběžné přímky (mimoběžky). Zápisem p \nparallel q pro přímky p, \ q v prostoru se rozumí, že nejsou rovnoběžné, tj. jsou buď různoběžné nebo mimoběžné.

Vzájemná poloha přímky a roviny
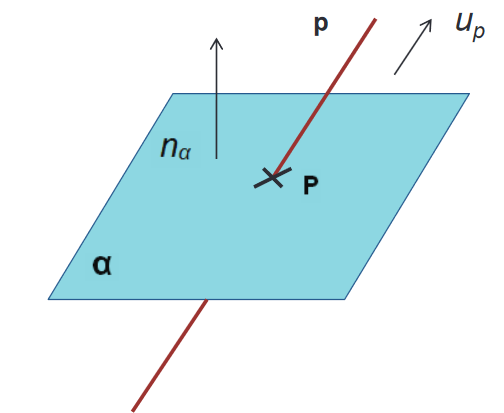
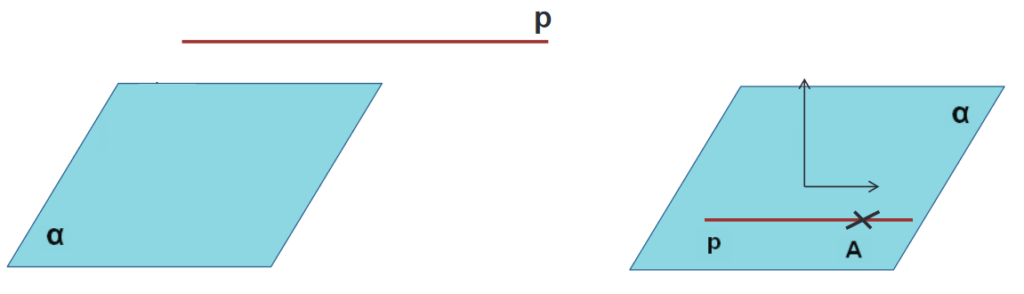
Vzájemná poloha přímky a roviny může být dvojí, a to: Neleží-li přímka p v rovině \varrho, má s ní (jak plyne z věty 2) společný nejvýše jeden bod. Jestliže má přímka p s rovinou \varrho společný právě jeden bod P, říkáme, že přímka p je různoběžná s rovinou \varrho. Bod P se pak nazývá průsečík přímky p s rovinou \varrho. Píšeme p \cap \varrho = \{ P \}. Píšeme p \nparallel q.
Nemá-li přímka p s rovinou \varrho žádný společný bod (p \cap \varrho = \varnothing) nebo leží-li v rovině \varrho (p \subset \varrho ), říkáme, že přímka p je rovnoběžná s rovinou \varrho. Píšeme p \parallel q.

Vzájemná poloha dvou rovin
Pro vzájenou polohu dvojice rovin jsou tyto možnosti: Dvě různoběžné roviny \varrho, \ \sigma, které mají společnou jednu přímku p, se nazývají různoběžné roviny. Přímku p nazýváme průsečnicí rovin \varrho, \ \sigma a píšeme \varrho \cap \sigma = p. Zapisujeme \varrho \nparallel \sigma.
Dvě různé roviny \varrho, \ \sigma, které nemají žádný společný bod, se nazývají rovnoběžné roviny. Je účelné pokládat také dvě splývající roviny \varrho, \ \sigma (\varrho = \sigma) za rovnoběžné roviny. Zapisujeme \varrho \parallel \sigma.


Volné ronoběžné promítání
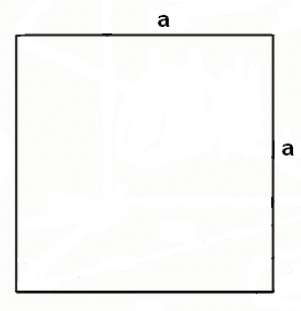
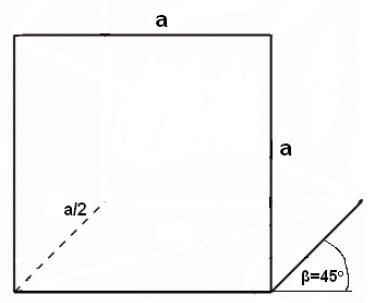
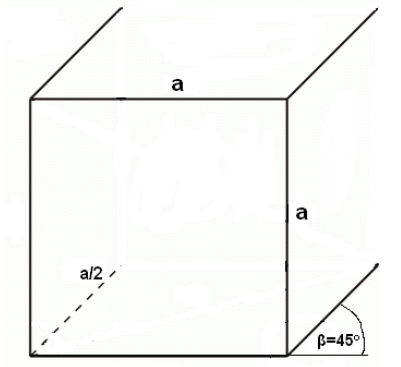
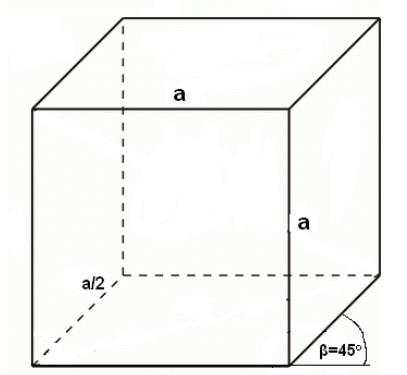
Než se pustíme do složitějších úloh jako vzájemná poloha rovin či řezy krychlí, měli bychom se naučit rovnoběžně promítnout tělesa do roviny. Na tomto promítání není v zásadě nic těžkého. Nejdříve si musíme určit průmětnu. Směr promítání je různoběžný s průmětnou. Útvary v této rovině (nebo rovnoběžné s touto rovinou) se zobrazují ve skutečné velikosti. Přímky kolmé na průmětnu se obvykle zobrazují s odchylkou 45° od vodorovného směru a jejich velikost je zmenšena o polovinu.
Postup promítnutí krychle ve volném rovnoběžném promítání (nadhled zprava):