Předpisem lineární funkce je výraz
f: \ y = ax + b, \ a, \ b \in \R
Příkladem lineární funkce může být například výraz
f: \ y=2x+1, kde a=2; \ b=1
Nebo také
f: y=4, kde a=0; \ b=4
Zaměřme se nejprve na definiční obor. Definičním oborem jsou všechna reálná čísla, což vidíme na první pohled z předpisu lineární funkce. Nejsme žádným způsobem omezeni volbou x. Nemáme zde žádný zlomek, kdybychom dělili nulou. Nemáme také žádnou odmocninu ani logaritmus. Nic zákeřného, čeho bchom se museli bát.
Definičním oborem každé lineární funkce jsou vždy reálná čísla.
Napišme si znovu zápis lineární funkce
f: \ y=ax+b ,
kde a je lineární člen a b je absolutní člen.
Přistupme ke grafu funkce. Grafem každé lineární funkce je vždy přímka. Každá přímka je určena právě dvěma body. Proto k určení grafu lineární funkce nám stačí vždy pouze dva různé body. Ty následně propojíme přímkou a získáme graf lineární funkce.
Pro f_1: \ y=2x+1 narýsujme graf funkce. Jak bylo zmíněno, pro kontrukci grafu lineární funkce (přímka) nám postačují pouze dva body. Body nalezneme nalezením průsečíků s osou x \ a \ y. Je možné použít jiné dva libovolné body, například výhodná je volba hodnot x = \{ 0; 1 \}
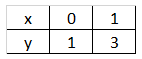
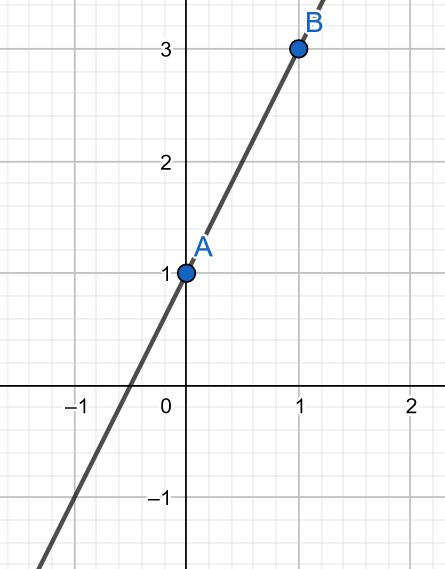
Průsečík s osou x získáme dosazením za y=0, tedy:
y = 2x+1 \\ 0 = 2x+1 \\ 2x = -1 \\ x = -\frac{1}{2}
Průsečíky o osami jsou:
x: \ [- \frac{1}{2};0] \\ y: \ [0;1]
Vidíme, že oborem hodnot jsou všechna reálná čísla, jako u každé lineární funkce (vyjma lineární funkce konstantní).
H_{f_1} = \R
Pro funkci f_{2}: y=-x+2 je opět definiční obor D_f = \R . Grafem lineární funkce je přímka, zvolíme si tedy dva libovolné body a dopočítáme příslušné funkční hodnoty.
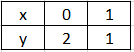
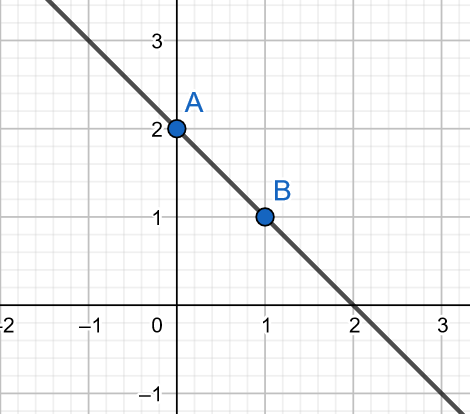
Průsečík s osou y vypočteme následovně:
y=-x+2 \\ 0=-x+2 \\ x=2
Průsečíky s osami jsou:
x: \ [2;0] \\ y: \ [0;2]
Vidíme, že oborem hodnot jsou všechna reálná čísla, jako u každé lineární funkce (vyjma lineární funkce konstantní).
H_{f_2} = \R
Zvláštním případem lineární funkce je funkce konstantní, která má lineární člen a = 0. Konstantní funkce ma tak tvar:
f: y = 0 \cdot x + b \Rightarrow y=b
Pozn.: Lineární člen ve tvaru 0 \cdot x se nepíše, je zde uveden pouze pro snažší nahlédnutí, kam dosazujeme všechny hodnoty x z definičního oboru funkce. Ať dosadíme libovolné x, tak přenásobené nulou mi dá opět nulu a funkce tak závisí pouze na absolutním členu b.
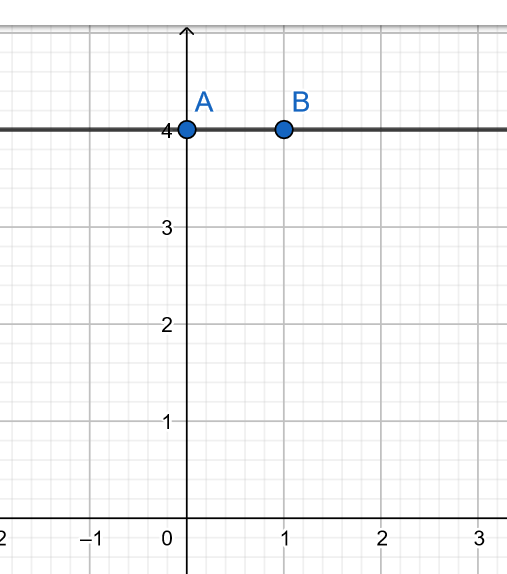
Mějme funkci f_3: y = 4. Definičním oborem jsou všechna reálná čísla. Do předpisu funkce mohu dosadit libovolné x. Jak bylo zmíněno výše, funkci si mohu přepsat takto:
f_3: \ y = 0 \cdot x + 4
tedy nejsem u definičního oboru konstantní funkce jakkoliv limitován a můžeme psát
D_{f_3} = \R
Dosadíme do tabulky hodnot:
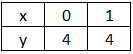
Vidíme, že po dosazení libovolné hodnoty za x dostaneme vždy hodnotu 4. A proto je grafem lineární konstantní funkce přímka rovnoběžná s osou x a oborem hodnot je hodnota absolutního členu, tedy
H_{f_3} = \{ 4 \}