S funkcemi lze provádět početní operace, konkrétně je lze sčítat, odčítat, násobit, a za určitých podmínek také dělit. Důležitou podmínkou při provádění těchto algeraických operací je, aby definiční obory funkcí nebyly vzájemně disjunktní, tj. výsledný definiční obor (součtu, rozdílu, ...) je průnikem jednotlivých definičních funkcí.
Pozn.: Definiční obory nejsou vzájemně disjunktní, tedy průnik definičních oborů je neprázdný (nevyjde prázdná množina).
Mějme následující funkce a proveďme na nich operaci součet, rozdíl, násobení a dělení.
f:y=x+2, x \in \langle -3 ; 6 \rangle \\ g:y=x^2-3, x \in \langle -2 ; 4 \rangle
nebo zapsáno jinak
f(x)=x+2, x \in \langle -3 ; 6 \rangle \\ g(x)=x^2-3, x \in \langle -2 ; 4 \rangle
Součet
f+g: \ y=(x+2)+(x^2-3)=x^2+x-1
lze také zapsat jinak
(f+g)(x)=f(x)+g(x)=(x+2)+(x^2-3)=x^2+x-1
Pro definiční obor výsledné funkce vzniklé součtem funkcí f, g platí:
D_{f+g} = D_f \cap D_g \\ D_{f+g} = \langle -3;6 \rangle \cap \langle -2;4 \rangle = \langle -2;4 \rangle
Jak vypadá část grafu funkce na grafu si můžete prohlédnout na následujícím obrázku. Všimněte si, že součet dvou funkcí není nic jiného, než součet jednotlivých funkčních hodnot v každé hodnotě x \in D_{f+g}
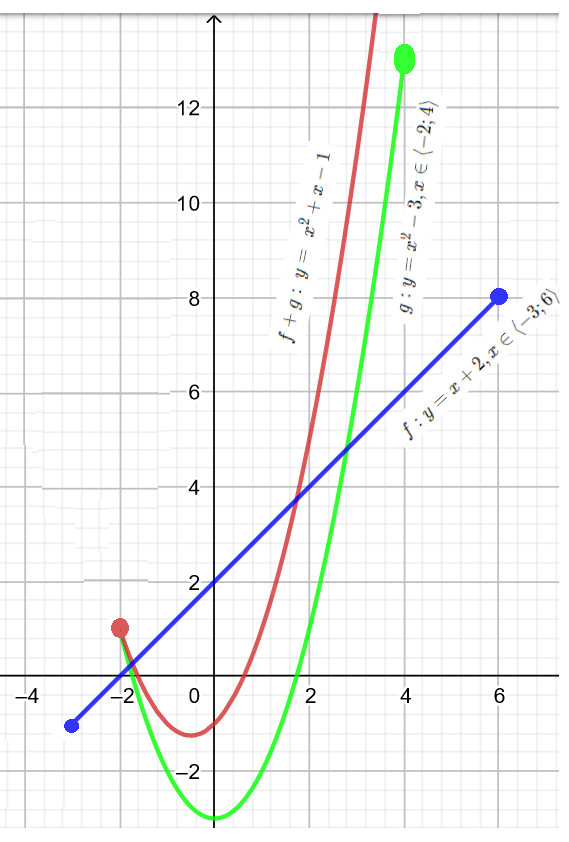
Rozdíl
f-g: \ y=(x+2)-(x^2-3)=-x^2+x+5
lze také zapsat jinak
(f-g)(x)=f(x)-g(x)=(x+2)-(x^2-3)=-x^2+x+5
Pro definiční obor výsledné funkce vzniklé rozdílem funkcí f, g platí:
D_{f-g} = D_f \cap D_g \\ D_{f-g} = \langle -3;6 \rangle \cap \langle -2;4 \rangle = \langle -2;4 \rangle
Jak vypadá část grafu funkce na grafu si můžete prohlédnout na následujícím obrázku. Všimněte si, že rozdíl dvou funkcí není nic jiného, než rozdíl jednotlivých funkčních hodnot v každé hodnotě x \in D_{f-g}
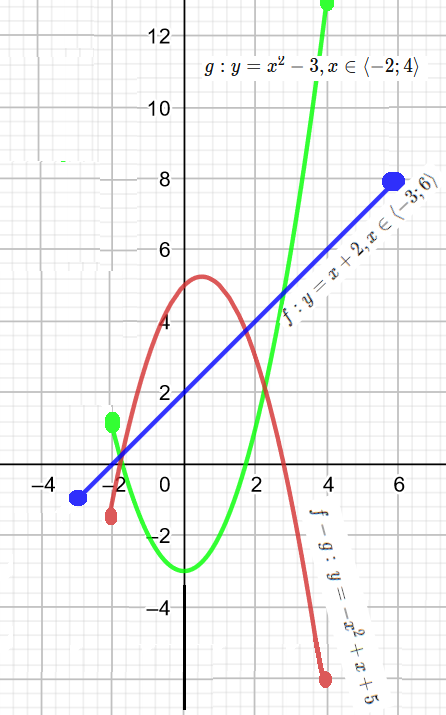
Součin
f \cdot g: \ y=(x+2) \cdot (x^2-3)=x^3+2x^2-3x-6
lze také zapsat jinak
(f \cdot g)(x)=f(x) \cdot g(x)=(x+2) \cdot (x^2-3)=x^3+2x^2-3x-6
Pro definiční obor výsledné funkce vzniklé součinem funkcí f, g platí:
D_{f \cdot g} = D_f \cap D_g \\ D_{f \cdot g} = \langle -3;6 \rangle \cap \langle -2;4 \rangle = \langle -2;4 \rangle
Jak vypadá část grafu funkce na grafu si můžete prohlédnout na následujícím obrázku. Všimněte si, že součin dvou funkcí není nic jiného, než součin jednotlivých funkčních hodnot v každé hodnotě x \in D_{f \cdot g}
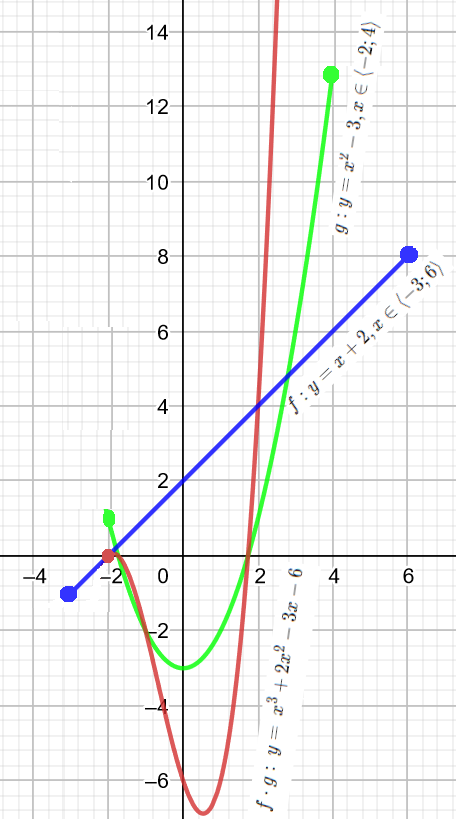
Podíl
\frac{f}{g}: \ y=\frac{x+2}{x^2-3}
lze také zapsat jinak
(\frac{f}{g})(x)=\frac{f(x)}{g(x)}=\frac{x+2}{x^2-3}
Pro definiční obor výsledné funkce vzniklé podílem funkcí f, g platí, že je průnikem definičních oborů funkcí f, g. Zároveň ale nesmí nastat situace, že se ve jmenovateli vyskytne nula. To nastane v případě, kdy
x^2-3 \neq 0 \\ x^2 \neq 3 \\ x \neq \pm \sqrt{3}
pak tedy platí
D_{\frac{f}{g}} = D_f \cap D_g - \{- \sqrt{3}; \sqrt{3} \} \\ D_{\frac{f}{g}} = \langle -3;6 \rangle \cap [\langle -2;4 \rangle - \{- \sqrt{3}; \sqrt{3} \} ] \\ D_{\frac{f}{g}} = \langle -2;4 \rangle - \{- \sqrt{3}; \sqrt{3} \}
Jak vypadá část grafu funkce na grafu si můžete prohlédnout na následujícím obrázku. Všimněte si, že podíl dvou funkcí není nic jiného, než podíl jednotlivých funkčních hodnot v každé hodnotě x \in D_{\frac{f}{g}}. Zároveň nesmí být funkce g rovna nule, to nastane v případě, kdy x = \pm \sqrt{3}. Na grafu funkce si můžete povšimnout, že v těchto dvou hodnotách není výsledná funkce definovaná. Funkce f, g však v těchto bodech definovány jsou.
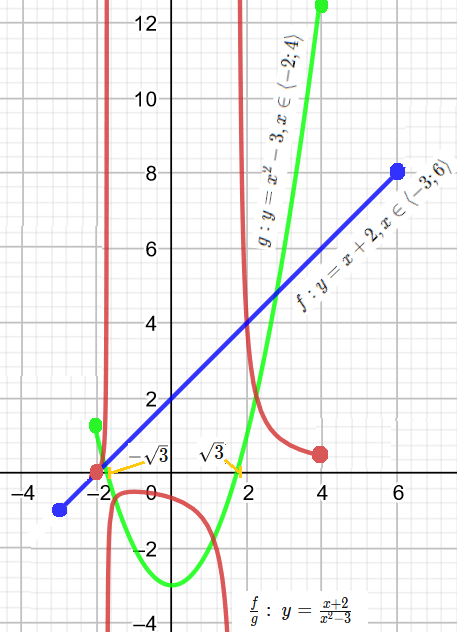
Rovnost funkcí
Abychom mohli říci, že jsou si dvě funkce rovny, musí platit dvě podmínky:
- Musí mít "stejný předpis".
- Musí mít stejný definiční obor.
V prvním bodě je napsáno "stejný předpis" v úvozovkách, jelikož předpisy nemusí být na první pohled totožné. Stejný předpis máme na mysli, že pro všechny hodnoty x nám vrátí funkce stejné hodnoty y.
Příklad:
f: y=x+1 \\ g: y=x^2-3Tyto funkce si na první pohled nejsou rovny. Mají sice stejné definiční obory, a to všechna reálná čísla, ale předpisy nevrací stejné hodnoty po dosazení libovolného x.
f(0) = 0+1 = 1 \\ g(0) = 0^2 - 3 = -3.
Vidíme, že v nule si funkce nejsou rovny. Našli jsme jeden sporný bod, tím pádem můžeme říci, že funkce si nejsou rovny.
f(x) \neq g(x)
Příklad:
f: y=1 \\ g:y=\frac{x}{x}Funkce f je rovna 1 na celém svém definičním oboru. Funkce g by bylo možné přepsat jako g: y=\frac{x}{x}=1 a vidíme, že po dosazení jakéhokoliv čísla bychom dostali opět hodnotu 1.
Na první pohled by se mohlo zdát, že funkce jsou si rovny, ale není tomu tak. Definiční obory se nerovnají, jelikož D_f=\R a D_g=\R - \{0\}. Funkce si tedy nejsou rovny.
f(x) \neq g(x)
Příklad:
Mějme funkce:
f:y=1 \\ g:y= \sin^2{x} + \cos^2{x}
Definičním oborek funkce f jsou všechna reálná čísla. Definičním oborem funkce g jsou také všechna reálná čísla.
Pozn.: Definiční obory goniometrických funkcí jsme ještě neprobírali, proto definiční obor prozradíme. V tomto případě nás zajímá stanovení rovnosti funkcí.
Upravme si funkci g ze znalosti funkcí \sin a \cos. Načrtněme si pravoúhlý trojúhelník a vyjádřeme si strany pomocí funkcí \sin a \cos.
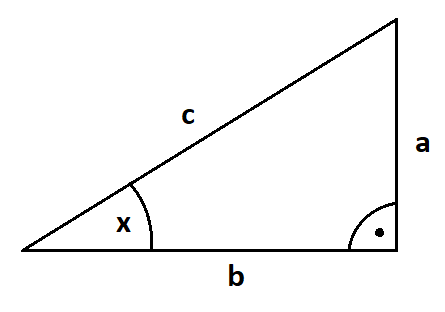
\sin(x) = \frac{a}{c} \\ \cos(x) = \frac{b}{c}
Umocníme a získáme:
\sin^2(x) = \frac{a^2}{c^2} \\ \cos^2(x) = \frac{b^2}{c^2}
Následně dosadíme do předpisu funkce g a upravíme zlomky. V čitateli pak máme námi známou Pythagorovu větu.
\sin^2(x) + \cos^2(x) = \frac{a^2}{c^2} + \frac{b^2}{c^2} = \frac{a^2 + b^2}{c^2} = \frac{c^2}{c^2} = 1
Můžeme tedy psát:
f:y=1 \\ g:y= \sin^2{x} + \cos^2{x}=1
Definiční obory jsou si rovny, proto platí, že jsou si funkce rovny.
f(x) = g(x)
Skládání funkcí
Mějme funkce
f:y=x-1 \\ g:y=\sqrt{x+1}
Určíme si definiční obory
D_f = \R \\ D_g = \langle -1 ; \infty )
Pokud chceme funkce složit, používáme kolečko \circ . Zápisem
(f \circ g)(x) = f(g(x))
rozumíme operaci, kdy funkci g vložím do funkce f. Čteme "f po g". Funkce f je funkce vnější. Funkce g je funkce vnitřní.
(f \circ g)(x) = f(g(x)) = f(\sqrt{x+1})
V dalším kroku odmocninu vložím za proměnnou x do funkce f. Tedy dostáváme:
(f \circ g)(x) = f(g(x)) = f(\sqrt{x+1})=\sqrt{x+1}-1
Nyní zkusme naopak složit "g po f", tedy
(g \circ f)(x)=g(f(x))
(g \circ f)(x)=g(f(x)) = g(x-1) = \sqrt{x-1+1} = \sqrt{x}
Nyní určíme ještě definiční obory složených funkcí:
(f \circ g)(x) = f(g(x)) = f(\sqrt{x+1})=\sqrt{x+1}-1 \\ D_{f \circ g} = \langle -1 ; \infty )
(g \circ f)(x)=g(f(x)) = g(x-1) = \sqrt{x-1+1} = \sqrt{x} \\ D_{g \circ f} = \langle 0; \infty ) = \R^+
Inverzní funkce
Inverzní funkce vyžaduje znalosti širšího spektra funkcí, jako například lineární, kvadratická, exponencionální, a dalších. Proto v této části si pouze nastíníme princip získávání inverzní funkce a její základní charakteristiku.
Důvodem, proč je tato látka zařazována do tohoto tematického celku je ten, že některé typy funkcí, které přijdou v budoucnu, budou motivovány tím, že jsou právě inverzní k nějaké jiné funkci, kterou již známe. Proto už nyní potřebujeme mít představu o pojmu inverzní funkce.
Mějme funkci f: \ y=2x-1, kterou lze přepsat jako f(x) = 2x-1. Nejprve si určíme graf této funkce a vytvoříme si tabulku funkčních hodnot.
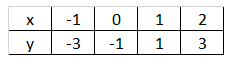
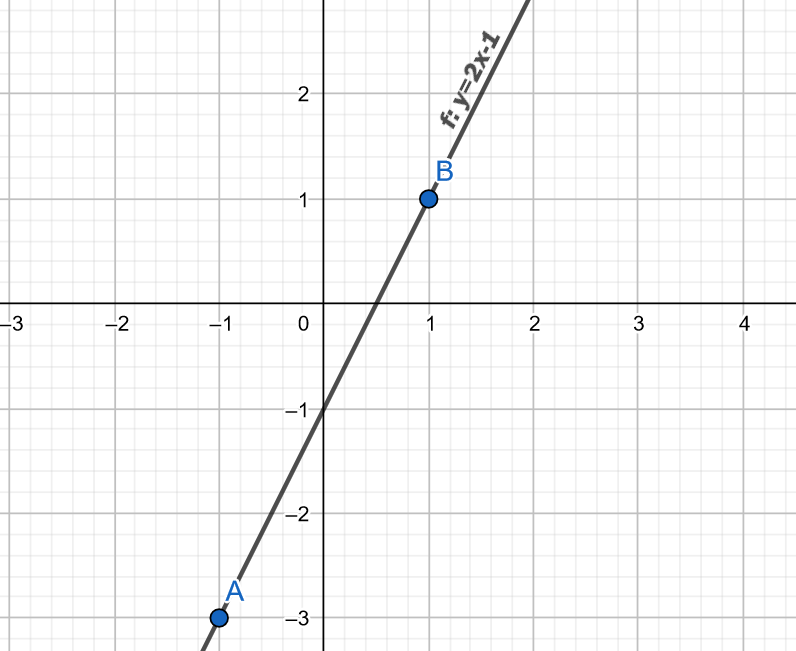
V předešlé kapitole jsme zmiňovali pojem prostá funkce. Funkce je prostá, pokud je jenom rostoucí nebo nejom klesající (ryze monotónní) na celém definičním oboru. Naše funkce je rostoucí na celém definičním oboru. A to je důležitý poznatek, protože inverzní funkci je možné naleznout pouze a jen tehdy, pokud je funkce ryze monotónní na celém definičním oboru.
Jakým způsobem inverzní funkci f^{-1} nalezneme? Do grafu si narýsujeme osu s předpisem y=x. Čím je tato funkce zajímavá? Funkce f je souměrná s funkcí f^{-1} podle osy y=x.
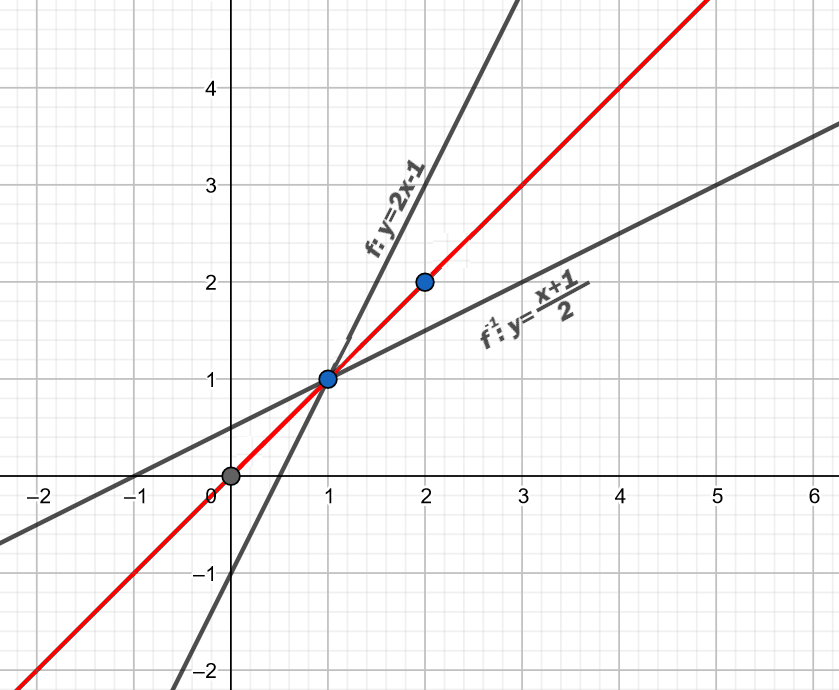
Jak nalezneme předpis? Vezmeme si předpis funkce f a zaměníme proměnné x \Leftrightarrow y . Následně vyjádříme y a získáváme inverzní funkci f^{-1}.
f: \ y=2x-1 \\ f^{-1}: \ x=2y-1 \\ f^{-1}: \ 2y = x+1 \\ f^{-1}: \ y=\frac{x+1}{2}
Zjistili jsme předpis inverzní funkce. Dosaďme si do předpisu funkce f^{-1} hodnoty z tabulky na začátku příkladu a tabulky si porovnejme:
f: \ y=2x-1
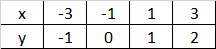
Všimněme si, že definiční obor funkce f odpovídá oboru hodnot inverzní funkce f^{-1}. A obor hodnot funkce f odpovídá definičnímu oboru inverzní funkce f^{-1}. Platí tedy:
D_f = H_{f^{-1}} \\ H_f = D_{f^{-1}}
To je také důvod, proč musí být funkce prostá. Pokud by byla funkce konstantní, tak by se zobrazila jako rovnoběžka s osou y. To by se ale nejednalo o funkci, protože by pro jednu hodnotu x bylo více hodnot y.
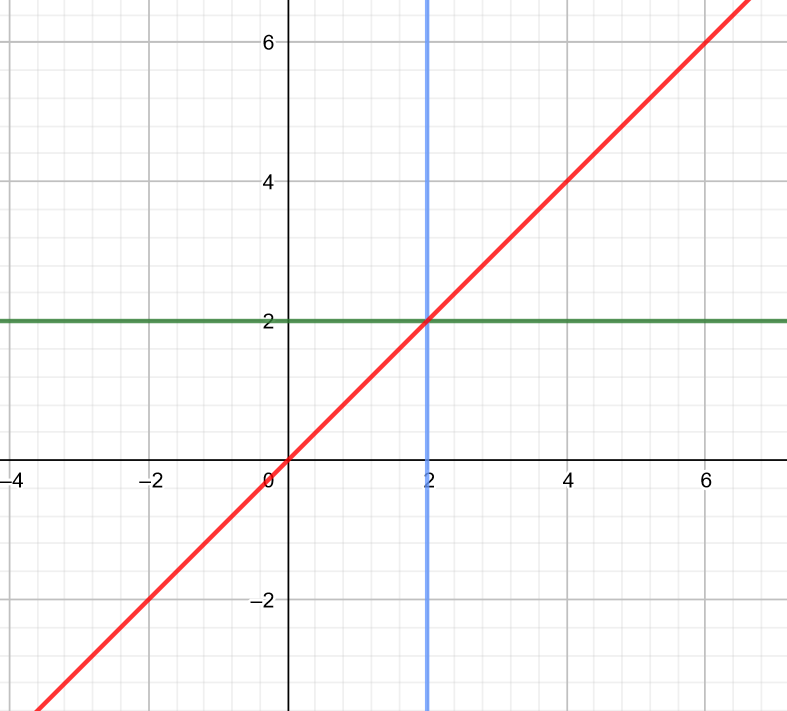
Pokud by funkce nebyla prostá (někdy roste, někdy klesá), inverzní křivka by nebyla funkcí, jelikož pro jednu hodnotu x bychom dostali více hodnot y. A to již není funkce!
Souvislost složené funkce a funkce inverzní
Platí, že pokud mám funkci inverzní a složím ji s funkcí původní, pak se tyto dvě funkce vyruší a získám pouze x, tedy osu souměrnosti. Tuto vlastnost využijeme v budoucnu při práci s exponenciálníma a logaritmickýma funkcema.
(f \circ f^{-1})(x) = x
Přesvědčme se:
(f \circ f^{-1})(x) = f(f^{-1}(x)) = f(\frac{x+1}{2}) = 2 \cdot (\frac{x+1}{2})-1 = x+1-1 = x
Složíme i druhým způsobem:
(f^{-1} \circ f)(x) = f^{-1}(f(x)) = f^{-1}(2x-1) = \frac{(2x-1)+1}{2} = \frac{2x}{2} = x
Opět vidíme, že složením funkce inverzní a funkce k ní původní získáváme předpis osy soměrnosti x.
Příklad
V dalším příkladech budeme hledat inverzní funkce, které ještě neznáme. Nám jde nyní ale o objasnění si principu nalezení inverzní funkce a dále o stanovení oboru hodnot a definičního oboru (pokud budeme schopni toto zjistit).
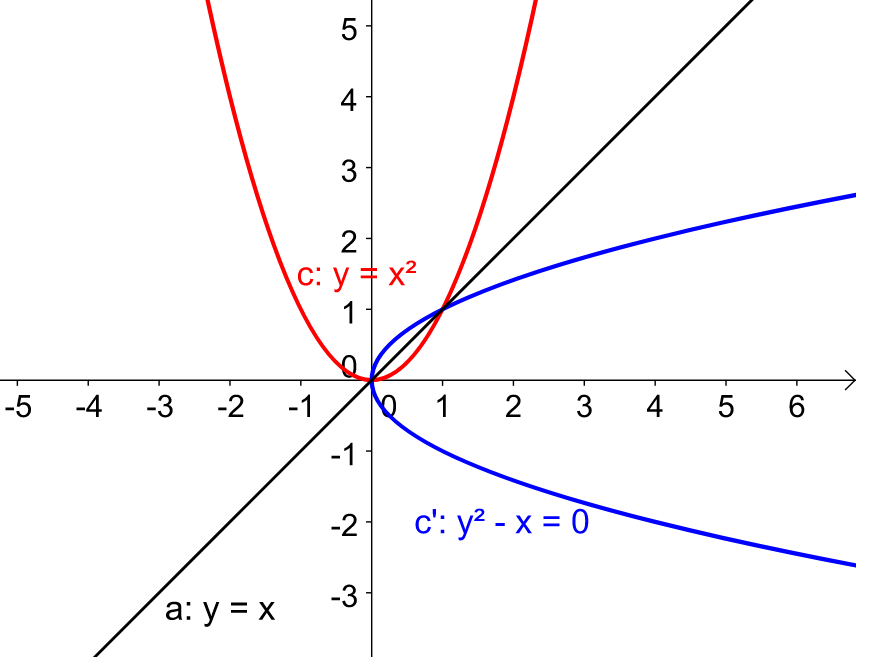
Mějme funkci f: \ y=x^3 a nalezněme inverzní funkci f^{-1}. Graf této funkce vypadá následovně a můžeme si všimnout, že se jedná o funkci lichou (souměrná podle počátku) a prostou (ryze monotónní, rostoucí na celém definičním oboru). Funkce je lichá, tedy existuje funkce k ní inverzní!!!

Zároveň také můžeme určit definiční obor funkce f. Jedná se o všechna reálná čísla. Tím pádem obor hodnot inverzní funkce budou také všechna reálná čísla. Platí tedy
H_{f^{-1}} = D_f = \R
Inverzní funkce bude s původní funkcí souměrná podle osy souměrnosti dané předpisem y = x. Můžeme si podobu inverzní funkce již narýsovat.
Vypočtení předpisu inverzní funkce:
f: \ y=x^3 \\ f^{-1}: \ x=y^3 \\ f^{-1}: \ y = \sqrt[3]{x}
Dalším využitím inverzní funkce je hledání oboru hodnot původní funkce. Definiční obor se ve většině případů určuje snázeji než obor hodnot. Stačí určit definiční obor inverzní funkce a získáme obor hodnot funkce původní. Platí tedy:
f^{-1}: \ y=\sqrt[3]{x} \\ D_{f^{-1}} = \R \Rightarrow H_f = D_{f^{-1}} = \R
Na závěr si ještě ověřme složením funkce a funkce k ní inverzní, zda výsledkem složení bude x.
(f \circ f^{-1})(x) = f(f^{-1}(x)) = f(\sqrt[3]{x}) = (\sqrt[3]{x})^3 = x
(f^{-1} \circ f)(x) = f^{-1}(f(x)) = f^{-1}(x^3) = \sqrt[3]{x^3} = x
Příklad
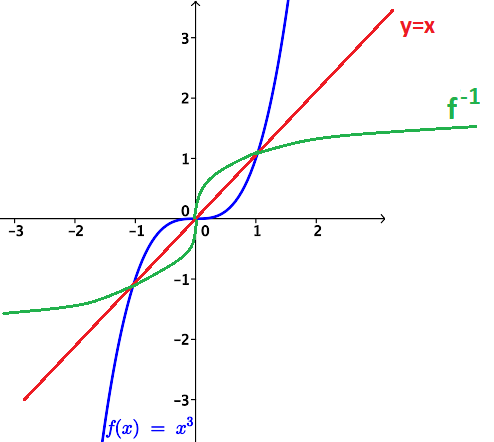
Vraťme se nyní k pojmu funkce prostá. Proč musí být funkce prostá, aby měla inverzní funkci? Podívejme se na následující příklad, co by se stalo, kdyby funkce nebyla ryze monotónní. Zkusíme najít funkci k ní inverzní.

Vidíme, že modrá funkce není funkcí, protože pro jedno x nalezneme dvě y. Proto musí být funkce prostá (ryze monotónní), aby k ní existovala funkce inverzní.
Zkusme početně:
f: \ y=x^2 \\ f^{-1}: \ x=y^{2} \\ f^{-1}: \ y = \pm \sqrt{x}
Všimněme si, že pro interval x \in (- \infty ; 0 \rangle je funkce f ryze monotónní (je klesající), tedy prostá. Našli bychom pro ni na tomto intervalu inverzní funkcí. Byla by jí funkce f^{-1}: \ y=- \sqrt{x}.
Pro interval x \in \langle 0 ; \infty ) je funkce f také ryze monotónní (je rostoucí), tedy prostá. Našli bychom pro ni na tomto intervalu inverzní funkcí. Byla by jí funkce f^{-1}: \ y= \sqrt{x}.
Na následujícím grafu je původní červená parabola rozdělena na dvě části, a to na intervaly (- \infty ; 0 \rangle ; \langle 0 ; \infty ) . Následně jsou barevně vyobrazeny inverzní funkce, kdyby původní funkce byla prostá. My jsme ji prostou neměli, nicméně mohli jsme původní funkci rozdělit tak, aby byla ryze monotónní, tedy prostá.
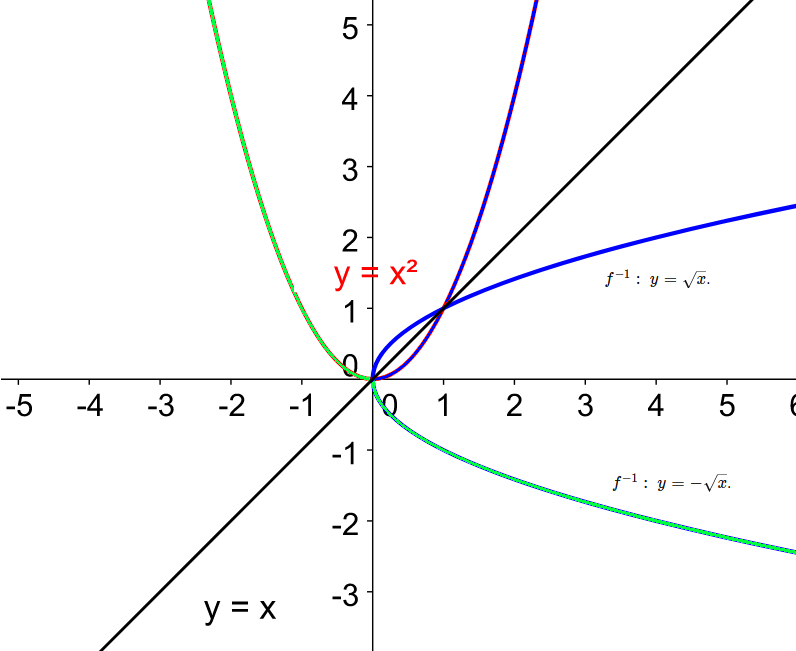
Nyní můžeme vypočíst obory hodnot a definiční obory. Platí:
f: y=x^2 \\ f^{-1} =- \sqrt{x}, x \in (- \infty ; 0 \rangle \\ f^{-1} = \sqrt{x}, x \in \langle 0 ; \infty )
Pro intervaly ( - \infty ; 0 \rangle \ a \ \langle 0 ; \infty ) platí:
D_f = ( - \infty ; 0 \rangle \Rightarrow H_{f^{-1}} = ( - \infty ; 0 \rangle \\ D_f = \langle 0 ; \infty ) \Rightarrow H_{f^{-1}} = \langle 0 ; \infty )
Dále také vidíme, že pod sudou odmocninou může být pouze nezáporné číslo, tedy platí:
x \in (- \infty ; 0 \rangle : \ D_{f^{-1}}: \ y=- \sqrt{x}, D_{f^{-1}} = \R_0^{+} \Rightarrow H_f = \R_0^{+} \\ x \in \langle 0 ; \infty ): \ D_{f^{-1}}: \ y = \sqrt{x}, D_{f^{-1}} = \R_0^{+} \Rightarrow H_f = \R_0^{+}
Pokud sjednodíme nyní získané hodnoty definičních oborů a oboru hodnot, zjistíme, že původní funkce má:
D_f: \ \R \\ H_f: \ \R_0^{+}