Mechanika patří k nejstarším odvětvím fyziky. Její základy vybudoval italský učenec Galileo Galilei (1564 - 1642) a anglický matematik a fyzik Isaac Newton (1642 - 1727).
Mechanika se zabývá studiem mechanického pohybu. Podle toho, jak na pohyb nahlížíme, dělíme mechaniku na dvě kategorie:
- Kinematika - zajímá se o popis pohybu (trajektorie, dráha, rychlost, ...) bez ohledu na důvody (síly), které těleso uvedlo do pohybu. Kinematika tedy zkoumá, jak se těleso (hmotný bod) pohybuje. Název kinematika pochází z řeckého slova kineó = pohybuji.
- Dynamika - zajímá se o příčiny pohybu tělesa (hmotného bodu), tj. o síly, které na těleso působí a uvedly ho do pohybu. Dynamika tedy zkoumá, proč se těleso pohybuje.
Abychom mohli zkoumat pohyb tělesa, je nutné zavést pojem vztažná soustava. Jedná se o soustavu těles, které jsou vzájemně v klidu a vůči nim popisujeme pohyb.
Soustava těles, ke kterým vztahujeme pohyb nebo klid sledovaného tělesa, se nazývá vztažná soustava.
Vztažnou soustavou mohou být tělesa skutečná (lampa u silnice, cestující stojící na nástupišti) nebo smyšlená (soustava souřadnic).
Několikrát byl použit pojem hmotný bod. Hmotným bodem ve fyzice nahrazujeme každé těleso, jehož rozměry jsou vzhledem ke zvolené vztažné soustavě zanedbatelné. Hmotný bod je charakterizován pouze hmotností, ale jeho vnitřní struktura již není podstatná.
Zavedením tohoto pojmu si ve fyzice zjednodušíme situace, které by v opačném případě vyžadovali brát v potaz aspekty neovlivňující pohyb nebo minimálně ovlivňující pohyb, jako například vnitřní složení, tvar (aerodynamika) apod.
Příklad: Tygra běhajícího po širé pláni je možné považovat za hmotný bod (HB), ale pokud bude tygr v kleci nákladního auta, pak již tygra považovat za HB nelze.
Relativnost klidu a pohybu
O tom, zda je těleso v klidu nebo pohybu, rozhoduje volba vztažné soustavy. Předmět ležící na sedadle jedoucího automobilu je v klidu vzhledem k vozidlu, ve kterém je umístěn. Pohybuje se ale vzhledem k povrchu Země. Tentýž předmět na sedadle stojícího automobilu je v klidu vzhledem k povrchu Země, ale společně se Zemí vykonává automobil i předmět otáčivý pohyb planety Země. Pokud by byl pozorovatel například na Měsíci, předmět a automobil by byly pro pozorovatele v pohybu.
Pohyb a klid je relativní.
Z předchozího příkladu můžeme říci, že absolutní klid neexistuje. Všechna tělesa na Zemi a ve vesmíru jsou v neustálém pohybu. Pohyb je tak základní vlastností všech objektů.
Příklad: Na podlaze jedoucího vlaku leží míč. Míč je vzhledem k sedačkám vlaku v klidu (pohybují se stejnou rychlostí i směrem jako vlak). Míč je ale vzhledem k pozorovateli, který stojí na nástupišti, v pohybu.
Poloha hmotného bodu
Pro popis polohy hmotného bodu vzhledem ke zvolené vztažné soustavě musíme znát jeho polohu v libovolném okamžiku jeho pohybu v libovolném čase. Tuto polohu určujeme obvykle pomocí pravoúhlé soustavy souřadnic, kterou spojujeme se zvolenou vztažnou soustavou.
Pravoúhlou soustavu souřadnic tvoří tři navzájem kolmé osy x, y, z procházející počátkem souřadnic O.
V této tzv. kartézské soustavě souřadnic určujeme polohu hmotného bodu podobně jako v geometrii. Poloha bodu A je např. určena souřadnicemi x=4\ m, y=3\ m, z=2\ m, což zapisujeme ve tvaru A=[4\ m; 3\ m; 2\ m].
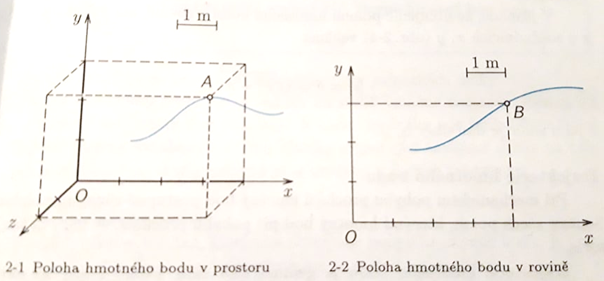
Polohu hmotného bodu vzhledem ke zvolené vztažné soustavě můžeme určit také pomocí polohového vektoru. Polohový vektor r znázorňujeme orientovanou úsečkou, jejíž počáteční bod O umisťujeme do počátku souřadnicové sosutavy a koncový bod do uvažovaného hmotného bodu. Souřadnice polohového vektoru jsou totožné se souřadnicemi hmotného bodu.
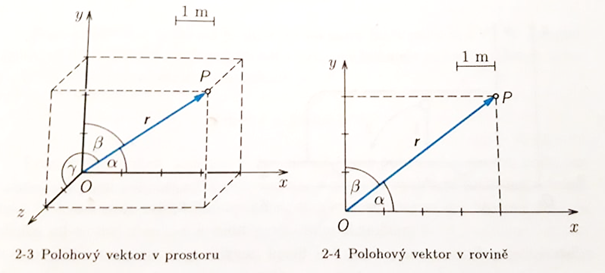
Polohový vektor |r| se rovná vzdálenosti hmotného bodu od počátku souřadnic O. Jsou-li souřadnice polohového vektoru x, y, z, pak pro jeho velikost platí vztah
|r|=r = \sqrt{x^2+y^2+z^2}
Směr polohového vektoru určují úhly \alpha, \beta, \gamma, které polohový vektor svírá s osami souřadnic.
V případě, že určujeme polohu hmotného bodu v rovině, má polohový vektor r o souřadnicích x, y, z velikost
|r|=r=\sqrt{x^2+u^2}
a jeho směr je dán úhly \alpha, \beta .
Příklady:
- Jsou dány souřadnice bodu A=[2;3;8]. Vypočti vzdálenost bodu od počátku soustavy souřadnic.
|r|=\sqrt{2^2+3^2+8^2}=\sqrt{4+9+64}=\sqrt{77} \doteq 8,77
Vzdálenost hmotného bodu od počátku soutavy souřadnic je \sqrt{77}. Ve fyzice se často vyskytují příklady, které vyjdou ve tvaru zlomku nebo odmocnin. Při složitějších výpočtech zaokrouhlejeme pouze konečný výsledek. Mezivýpočty ponecháváme v "ošklivém", ale zato přesném tvaru. Je také přesnější uvádět jako výsledek \sqrt{77} a výsledek tak nezaokrouhlovat. Při další práci s výslednou hodnotou pak máme její přesný tvar.
Trajektorie
Trajektorií nazveme souvislou čáru, kterou při svém pohybu kopíruje pohyb hmotného bodu. Trajektorii dle tvaru pohybu dělíme na:
- Trajektorie přímočará - grafem je přímka nebo úsečka. Příkladem takového pohybu může být pád kamene nebo rovně letící letadlo.
- Trajektorie křivočará - grafem je libovolná křivka. Jedná se o pohyb, který není přímočarý. Příkladem může být letící pták, slalomář, psaní perem. Zvlášním případem je pak pohyb po kružnici (trajektorie je kružnice). Příkladem je pohyb Země kolem Slunce.
Délku trajektorie, kterou hmotný bod urazí za čas t, značíme s nebo se můžeme setkat se zápisem s(t). Tento zápis nám říká, že veličina dráha je závislá na veličině čas.
Rychlost
Okamžitá rychlost v hmotného bodu v čase t definujeme jako přírustek dráhy \Delta s, k němuž dojde za čas \Delta t . Zároveň časový okamžik je velmi malý \Delta t \rightarrow 0 . Pro okamžitou rychlost platí vztah:
v=\frac{\Delta s}{\Delta t}
Jednotkou okamžité rychlosti je m \cdot s^{-1}, setkáváme se i se zápisem ve tvaru zlomku \frac{m}{s}. V praxi se často používá také jednotka km /cdot h nebo km \cdot h^{-1}.
Převodní vztah: 1 \ m \cdot s^{-1} = 1 \ \frac{m}{s} = \frac{ \frac{1}{1000} \ km}{\frac{1}{3600} \ h} = \frac{3600}{1000} \frac{km}{h} = 3,6 \ km \cdot h^{-1}
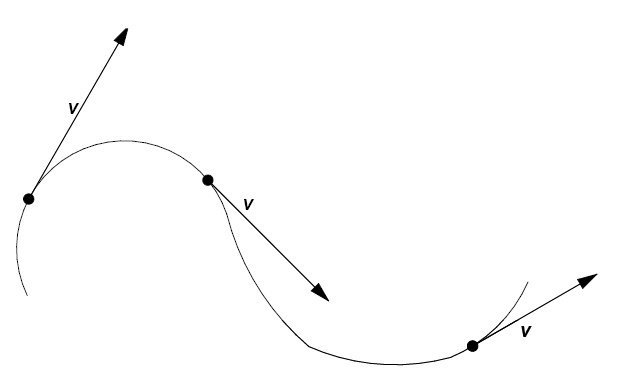
Okamžitá rychlost je vektorová veličina, která má velikost a směr. Má vždy směr tečny k dané trajektorii bodu.
Příklad: Převeď 200\ \frac{m}{s} na jiné jednotky.
Při řešení tohoto ilustrativního příkladu si ukážeme, jak jednoduše převádět jednotky rychlosti, pokud nemůžeme využít koeficient 3,6. Ten je využitelný pouze a jen tehdy, pokud převádíme z metrů za sekundu na kilometry za hodinu (\cdot \ 3,6) nebo z kilometrů za hodinu na metry za sekundu (:3,6).
200\ \frac{m}{s} = 0,2\ \frac{km}{s}
Platí, že 1\ km = 1000\ m. Proto číslo 200 vidělím 1000.
0,2\ \frac{km}{s} = 12\ \frac{km}{min}
Platí, že 1\ min = 60\ s. Proto číslo 0,2 vynásobíme 60. Proč vynásobíme? Protože se čas nachází ve jmenovateli a snadno nahlédneme, že pokud urazím za jednu sekundu 0,2\ km, pak za minutu to bude 60x více.
Stejným postupem převádíme na libovolné jednotky.
200\ \frac{m}{s} = 0,2\ \frac{km}{s} = 12\ \frac{km}{min} = 720\ \frac{km}{h}
200\ \frac{m}{s} = 2\ 000\ \frac{dm}{s} = 20\ 000\ \frac{cm}{s} = 200\ 000\ \frac{mm}{s}
Výpočet okamžité rychlosti
Průměrná rychlost
Průměrná rychlost v_{p} je definována jako celková dráha s, kterou těleso urazí za celkový čas t. Platí tedy:
v_{p} = \frac{s}{t}
Pozor, průměrná rychlost není tentýž pojem jako okamžitá rychlost. Průměrná rychlost běžce bude jiná, pokud poběží prvních 10 km do kopce a dalších 10 km z kopce. Pokud ale budeme zkracovat časový úsek, po který měříme průměrnou rychlost, dostaneme se k rychlosti okamžité. Tento časový úsek ale musí být velice krátký.
Příklad: průměrná rychlost
Podle velikosti okamžité rychlosti pak dělíme pohyb na:
- rovnoměrný - velikost rychlosti je konstantní a těleso urazí v libovolných úsecích trajektorie stejnou dráhu, pokud bereme stejné časové úseky.
- nerovnoměrný - jedná se o pohyb tělesa, kdy se velikost rychlosti s časem mění.
Rozměrová zkouška
Všimněme si, že okamžitá rychlost je dána vztahem v=\frac{s}{t} a jednotkou je pak \frac{m}{s}. Někdy není nutné si pamatovat samotný vzorec, jelikož jde odvodit z jednotky dané veličiny.
Kupříkladu rychlost má jednotku \frac{m}{s}. V čitateli se nachází jednotka pro dráhu, tedy s. Ve jmenovateli je pak jednotka pro čas, tedy t. Z jednotky jsem schopen odvodit vzorec pro výpočet rychlosti. Tomuto postupu a kontrole zároveň se říká rozměrová zkouška.
v=\frac{s}{t} \sim \frac{m}{s}
Dalším příkladem rozměrové zkoušky může být jednotka Newton, který odpovídá
F \sim N \sim \frac{kg \cdot m}{s^2}
Kilogram je jednotka hmotnosti, tedy m. Výraz \frac{m}{s^2} odpovídá zrychlení {katex]a[/katex]. Můžeme tedy psát, že
F \sim N \sim \frac{kg \cdot m}{s^2} \sim kg \cdot \frac{m}{s^2} \Rightarrow F=m \cdot a
Grafické znázornění dráhy na čase
Základní jednotkou dráhy je metr a značí se m, což lze zapsat takto: s[m]. Dráha je závislá na době trvání pohybu. Souvislost dráhy a času lze graficky interpretovat takto:
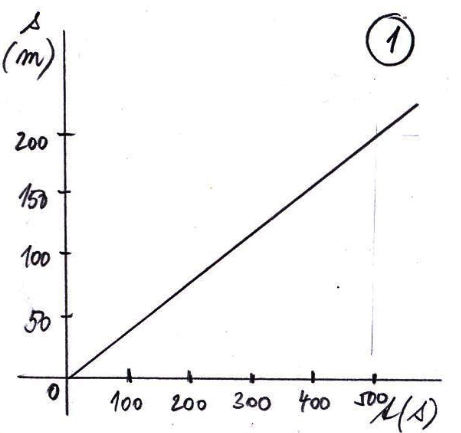
Jedná se o graf závislosti dráhy na čase. Čas je na ose x uveden v sekundách. Dráha je uvedena na ose y v metrech. Tabulka pro odečítání hodnot pak vypadá následovně

Jedná se o rovnoměrný pohyb, při kterém za každých 100 sekund urazí těleso 40 metrů. Průměrná rychlost je pak 0,4 \frac{m}{s}.
Grafické znázornění rychlosti na čase
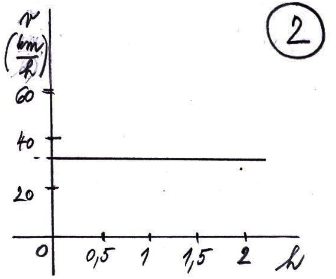
Jedná se o graf závislosti rychlosti na čase. Čas je uveden v hodinách, rychlost je uvedena v kilometrech za hodinu. Jedná se o rovnoměrný pohyb pro konstantní rychlosti 33 \frac{km}{h}.

Pokud vypočteme plochu pod křivkou, dostaneme celokovou ujetou vzdálenost za určitý čas, po který se vozidlo pohybovalo. V našem případě bude platit, že s=v \cdot t = 33 \cdot 2 = 66\ km.
Opět nám vychází rozměrová zkouška, proto6e
s(km) \sim \frac{km}{h} \cdot h \sim \frac{km \cdot h}{h} \sim km
Grafické znázornění dráhy na čase
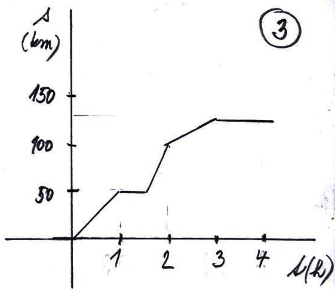
Jedná se o graf závislosti dráhy na čase. Čas je uveden v hodinách, dráha je uvedena v kilometrech. Rozbor grafu:
- 0 h - 1 h se pohybuje automobil rovnoměrným pohybem, ujel 50\ km
- 1 h - 1,5 h je automobil v klidu (stojí)
- 1,5 h - 2 h se automobil pohybuje rovnoměrným pohybem a ujel 50\ km
- 2 h - 3 h se automobil pohybuje rovnoměrným pohybem a ujel 25\ km
- 3h - 4 h automobil stojí (je v klidu)
Celkem tak automobil urazil 125\ km.
Příklady - průměrná rychlost + rovnoměrný přímočarý pohyb
Karel a Adam šli na výlet. Karel šel nejdříve dvě hodiny stálou rychlostí o velikosti 4\ \frac{km}{h} a pak dvě hodiny stálou rychlostí 1\ \frac{km}{h}. Adam šel nejdříve dvě hodiny stálou rychlostí o velikosti 3\ \frac{km}{h} a pak stálou rychlostí o velikosti 4\ \frac{km}{h}. Určete
- Jakou dráhu každý z chlapců urazil?
- Jaké jsou průměrné rychlosti obou chlapců během výletu?
Řešení: Oba urazili 10\ km. Karlova průměrná rychlost byla 2,5\ \frac{km}{h}, Adamova průměrná rychlost byla 3,3\ \frac{km}{h}.
Zdroj: http://reseneulohy.cz/1150/prumerna-rychlost-chuze
Z místa A plave proti proudu řeky loďka do místa B. Rychlost loďky vzhledem k vodě je v obou případech stejná, a to 4\ \frac{km}{h}. Rychlost proudu je 1,6\ \frac{km}{h}. Určete poměr doby, za kterou vykoná loďka dráhu z místa A do místa B a zpět, a doby, kterou by loďka potřebovala na vykonání této dráhy po jezeře.
Řešení: Poměr doby je \frac{16}{13,44} \doteq 1,19
Zdroj: http://reseneulohy.cz/106/pohyb-lodky
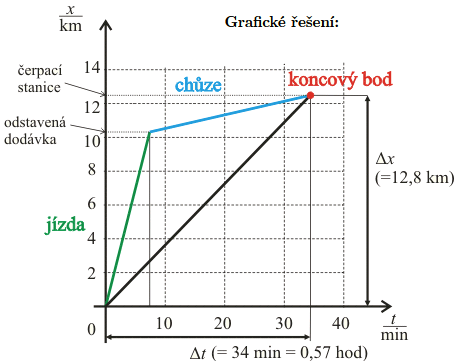
Nákladní dodávka jede po přímé silnici stálou rychlostí 86\ \frac{km}{h}. Po ujetí 10,4\ km náhle dojde palivo. Řidič pokračuje pěšky v původním směru. za 27 minut dojde k čerpací stanici, vzdálené od dodávky 2,4\ km. Jaká je průměrná rychlost řidiče od chvíle, kdy vyjel s dodávkou z výchozího místa, až do okamžiku příchodu k čerpací stanici?
Řešte výpočtem i graficky.
Řešení: Průměrná rychlost je směrnicí přímky spojující výchozí bod a koncový bod, tedy v_p = \frac{12,8\ km}{0,57\ h} \doteq 22\ \frac{km}{h}.
Průměrná rychlost je přímka a směrnicí přímky y=kx+b je koeficient k. Začínáme od nuly, proto koeficient b=0.