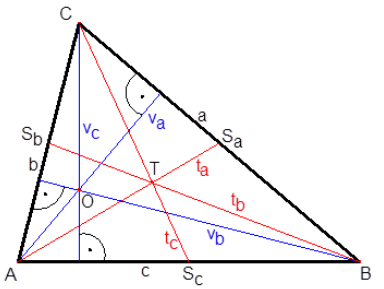
- A, B, C ... vrcholy
- a, b, c --- strany
- \alpha, \beta, \gamma --- vnitřní úhly. Platí: \alpha + \beta + \gamma = 180°
- v_a, v_b, v_c ... výšky (spojnice vrcholu se středem protější strany).
- O ... ortocentrum (průsečík výšek)
- t_a, t_b, t_c ... těžnice (spojnice vrcholu se středem protější strany)
- T ... těžíště (průsečík těžnic, rozdělí těžnice v poměru 1:2)
|S_a T| = \frac{1}{3} |S_a A|
|AT| = \frac{2}{3} |S_a T|
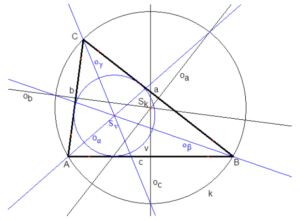
- Střed kružnice opsané trojúhelníku - průsečík os stran
- V případě tupoúhlého trojúhelníka je střed kružnice opsané vně trpjúhelníka.
- V případě pravoúhlého trojúhelníka leží střed kružnice opsané na přeponě trojúhelníka.
- V případě ostroúhlého trojúhelníka je střed kružnice opsané uvnitř trojúhelníka.
- Střed kružnice vepsané trojúhelníku - průsečík os úhlů
- V případě tupoúhlého, pravoúhlého i ostroúhlého trojúhelníka je střed kružnice vepsané vždy uvnitř trojúhelníka.
Střední příčky - spojnice středů stran
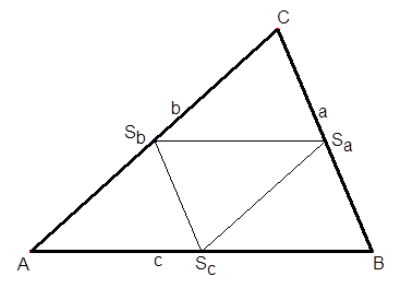
Vlastnosti středních příček:
- mají poloviční velikost než příslušná strana
- jsou rovnoběžné s příslušnou stranou
- dělí trojúhelník na čtyři shodné trojúhelník
Typy trojúhelníků
- Rozdělení podle délky stran:
- různostranný (obecný) - tři různé dlouhé strany
- rovnoramenný - dvě strany shodné (ramena) a třetíí různě dlouhá (základna)
- rovnostranný - tři shodné strany
- Rozdělení podle velikosti vnitřních úhlů
- ostroúhlý - všechny vnitřní úhly jsou ostré
- pravoúhlý - jeden vnitřní úhel je pravý
- tupoúhlý - jeden vnitřní úhel je tupý