Odmocniny
Odmocňování je inverzní operace k umocňování. Nejčatěji pracujeme s druhou odmocninou, která hledá takové číslo, které když vynásobíme se sebou samým, tak získáme původní číslo, které jsme odmocnili.
Druhá odmocnina
Pro odmocninu se používá znak \sqrt{}, konkrétně například druhá odmocnina z čísla 25 se zapíše jako \sqrt{25}. Nejprve se budeme zabívat druhou odmocninou reálného čísla. Definovali bychom ji takto:
\sqrt{a} \cdot \sqrt{a} = a
Pokud vynásobíte odmocninu čísla a s odmocninou čísla a, pak dostanete číslo a. Takže pro číslo 9 by odmocnina byla rovná 3, protože platí 3 \cdot 3 = 9.
Předchozí výraz můžeme také napsat takto:
(\sqrt{a})^2 = a
Je to jen jiný zápis předchozího násobení, a sice pomocí mocniny.
Podstatným faktem je, že tato rovnice platí jen pro ta x, která jsou z definičního oboru odmocniny. Platí totiž, že nemůžeme odmocnit záporné číslo. Můžeme odmocnit jakékoliv kladné číslo, můžeme odmocnit nulu, ale neumíme odmocnit záporné číslo? Proč to nejde?
Předpokládejme, že chceme vypočítat odmocninu z −25. Máme v zásadě dvě možnosti, jaké číslo zvolit. Buď kladné, nebo záporné. Pokud zvolíme kladné, máme 5 \cdot 5 = 25. Sice jsme dostali 25, ale my chceme −25. Zkusíme tak zvolit −5; jenže po vynásobení máme opět 25. Zkrátka pokud vynásobíte dvě záporná čísla, získáte číslo kladné. Stejně tak, když násobíte dvě kladná čísla. Museli byste násobit −5 \cdot 5, abyste získali −25 a to nejde, násobíte dvě různá čísla, byť se liší jen ve znaménku. Proto nelze vypočítat odmocninu ze záporného čísla.
Vícenásobná odmocnina
Podobně jako můžeme umocnit výraz na druhou, na třetí, na čtvrtou, můžeme mít i třetí a čtvrtou a nakonec n-tou odmocninu z reálného čísla. Zapisuje se to obvykle nad zobáček, takto:
\sqrt[5]{32}
Tento zápis značí pátou odmocninu z čísla třicet dva. n-tou odmocninu nadefinujeme pomocí n-té mocniny takto:
\sqrt[n]{a} = b \Longleftrightarrow b^n = a
Pokud za n dosadíme dva, získáváme druhou odmocninu tak, jak jsme si ji definovali před chvílí. Zkráceně bychom to mohli definovat i takto:
(\sqrt[n]{a})^n = a
Platí konvence, že pro druhou odmocninu tam nemusíme psát dvojku, tedy tyto zápisy jsou ekvivalentní:
\sqrt{64} = \sqrt[2]{64}
Takže například pro čtvrtou odmocninu by platilo:
\sqrt[4]{a} \cdot \sqrt[4]{a} \cdot \sqrt[4]{a} \cdot \sqrt[4]{a} =a
A nějaký konkrétní příklad:
\sqrt[3]{64} = 4
A naopak platí:
4 \cdot 4 \cdot 4 = 64
Odmocnina ze záporného čísla
Už víme, že neexistuje druhá odmocnina ze záporného čísla, protože a^2, kde a je reálné číslo, nikdy nebude záporné. Nicméně u vícenásobných odmocnin už nenásobíme pouze dvakrát, takže mohou nastat případy, kdy n-tá odmocnina ze záporného čísla existuje. Jak to tedy je?
Vadilo nám, že když dvakrát vynásobíme záporné číslo, získáme číslo kladné. Pro výsledek −25 jsme potřebovali součin −5 \cdot 5. Jenže co se stane, když násobíme tři záporná čísla? Po vynásobení prvních dvou záporných čísel máme kladné číslo. Ale po vynásobení posledním záporným číslem máme zpět záporné číslo. Pokud bychom násobili ještě jednou (celkem čtyřikrát), jsme zpět v kladných číslech.
Poučení je z toho takové, že pokud n-krát násobíme záporné číslo, tak když je n sudé, je výsledný součin kladný, když je liché, je součin záporný. Z toho vyvodíme, že existuje n-tá odmocnina ze záporného čísla, když je n liché. Příklad:
\sqrt[n]{-216} = -6
Pravidla pro počítání s odmocnimami
Nechť \forall a, b \in \R, \forall m, n \in \N:
\sqrt[n]{a} \cdot \sqrt[n]{b} = \sqrt[n]{a \cdot b}
\sqrt[3]{5} \cdot \sqrt[3]{7} = \sqrt[3]{5 \cdot 7} = \sqrt[3]{35}\frac{\sqrt[n]{a}}{\sqrt[n]{b}} = \sqrt[n]{\frac{a}{b}}, b \neq 0
\frac{\sqrt[3]{5}}{\sqrt[3]{7}} = \sqrt[3]{\frac{5}{7}}, b \neq 0(\sqrt[n]{a})^m = \sqrt[n]{a^m}
(\sqrt[3]{5})^6 = \sqrt[3]{5^6}\sqrt[m]{\sqrt[n]{a}} = \sqrt[mn]{a}
\sqrt[3]{\sqrt[4]{5}} = \sqrt[3 \cdot 4]{5} = \sqrt[12]{5}\sqrt[n]{a} = \sqrt[n \cdot p]{a^p}
\sqrt[3]{5} = \sqrt[3 \cdot 4]{5^4}Dále platí: \forall p, n \in \N, \forall a \in \R_0^+:
\sqrt[n]{a_1} \cdot \sqrt[n]{a_2} \cdot ... \cdot \sqrt[n]{a_p} = \sqrt[n]{a_1 \cdot a_2 \cdot ... \cdot a_p}
\sqrt[3]{4} \cdot \sqrt[3]{5} \cdot \sqrt[3]{6} = \sqrt[3]{4 \cdot 5 \cdot 6} = \sqrt[3]{120}\sqrt{a^2} = \vert a \vert
\sqrt{3^2} = \vert 3 \vertPříklady na počítání s odmocninami
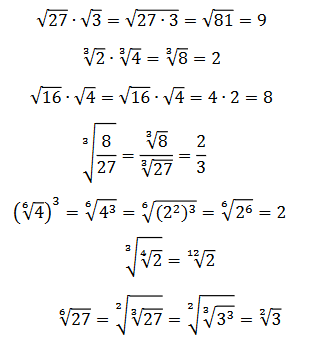
Příklady na částečné odmocnění
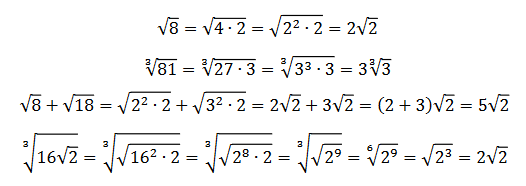
Příklady: