Existují ještě dvě další goniometrické funkce, tangens a kotangens. Hlavní rozdíl oproti předchozím goniometrickým funkcím je ten, že tangens a kotangens pracuje pouze s odvěsnami, nepracuje s přeponou.
Tangens úhlu \alpha se rovná poměru délky protilehlé odvěsny ku délce přilehlé odvěsny. Tangens obvykle značíme buď tg nebo tan. Častěji se ale užívá tg.
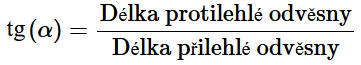
Cotangens úhlu \alpha se rovná poměru délky přilehlé odvěsny ku délce protilehlé odvěsny. Cotangens obvykle značíme cot nebo cotg. Častěji se ae užívá cot .
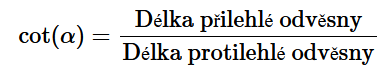
Důležité: Všimněte si, že funkce tangens a cotangens jsou v zásadě totožné. Zlomek pouze převrátíme. V praxi budete využívat pouze funkci tangens, cotangens je funkce navíc. Pokud příklad bude možné vypočítat pomocí funkce tangens, VŽDY tento příklad bude možné také vypočítat pomocí funkce cotangens.
Terminologie je opět stejná jako v předchozích částech i další práce s funkcemi je stejná. Vraťme se k předchozímu příkladu a zkusme vypočítat délku strany c jen ze znalosti velikosti úhlu \alpha a délky strany a, která je a = 3.

Tangens je poměr protilehlé odvěsny ku přilehlé odvěsně, takže matematicky zapsáno to bude vypadat takto:
tan(\alpha) = \frac{a}{c}
Potřebujeme vypočítat délku strany c, takže musíme z této rovnice osamostatnit výraz c. Vynásobíme výrazem c a vydělíme tan(\alpha) , podobně jako v předchozích příkladech.
\tan(\alpha) =\frac{a}{c}
\tan ( \alpha ) \cdot c = a
c = \frac{a}{\tan(\alpha)}
c = 3 \cdot \tan(30°)
Tangens 30° je roven přibližně 0,5774.
c = \frac{3}{0,5774} = 5,196 cm
Pro tangens třicet stupňů existuje tabulková hodnota, platí, že:
\tan (\alpha) = \frac{\sqrt{3}}{3}
takže předchozí výpočet můžeme vypočítat přesně
c = \frac{3}{\frac{\sqrt{3}}{3}} = 3 \cdot \frac{3}{\sqrt{3}} = \frac{9}{\sqrt{3}} = 5,196 cm
Tabulkové hodnoty
Sinus, cosinus, tangens a cotangens mají pro některé hezké úhly hezké výsledné hodnoty. Zde je jejich základní přehled:
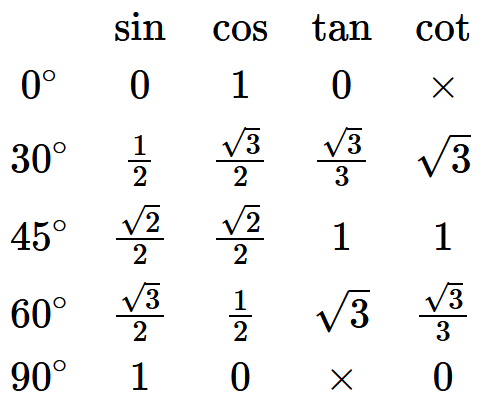
Pokud bysme stejným způsobem počítali s funkcí cosinus, dojdeme ke stejnému výsledku.
Příklady: