Reálná čísla a iracionální čísla
Pokud zobrazíme všechna racionální čísla na číselnou osu, tak i potom zůstanou na číselné ose neobsazená místa.
Reálné číslo: Reálnými čísly nazýváme čísla, která vyjadřují délky úseček, čísla k nim opačná a nulu. Každé reálné číslo je na číselné ose znázorněno právě jedním bodem. Každý bod číselné osy je obrazem právě jednoho reálného čísla.
Iracionální číslo: Iracionální číslo lze zapsat pouze jenom takovým desetinným rozvojem, který je nekonečný a neperiodický. Iracionální číslo nelze zapsat ve tvaru \frac{p}{q} , jako tomu je u čísel racionálních.
Slovo iracionální neznamená nerozumové, ale nepodílové. Příkladem iracionálního čísla je například Ludolfovo číslo \pi , některé odmocniny jako \sqrt{2}, \sqrt{3}, \sqrt{5} nebo čísla s neukončeným neperiodickým rozvojem 5,235 124 623 452 ...
Značení:
\R obor reálných čísel
\R^+ obor kladných reálných čísel
\R^- obor záporných reálných čísel
\R^+_0 obor kladných reálných čísel včetně nuly
\R^-_0 obor záporných reálných čísel včetně nuly
\R-Q nebo \R/Q obor iracionálních čísel
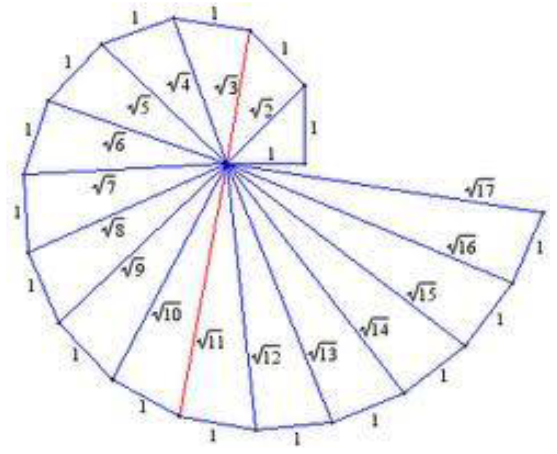
Konstrukce odmocniny - Euklidův šnek
Konstrukce vychází zpravoúhlého trojúhelníka a Pythagorovy věty. Jako první narýsujeme pravoúhlý trojúhelník s délkou odvěsen 1 a 1. Přepona je následně \sqrt{2}. Tuto přeponu využijeme nyní jako odvěsnu dalšího pravoúhlého trojúhelníka. Druhá odvěsna bude mít opět délku 1. Potom přepona bude mít délku \sqrt{3}, protože:
c^2 = 1^2 + (\sqrt{2})^2
c^2=1+2
c=\sqrt{3}
V praxi se často iracionální čísla nahrazují desetinnými, která jsou tvořena části desetinného rozvoje zaokrouhleného na stanovený počet číslic, jenž je určen požadovanou přesností výsledku.
Číslo zaokrouhlímena místo daného řádu tak, že vynecháme všechny číslice, které jsou v pravo od číslice na místě daného řádu, a je-li první z vynechaných číslic:
- menší než 5, pak všechny ponechané číslice se nemění
- rovna nebo větší jak 5, pak kčíslu tvořenému ponechanými číslicemi přičteme jednu jednotku nejmenšího ponechaného řádu
Příklady: