Doplněk množin
Mějme dvě množiny A a B, kde navíc platí B \subseteq A. V takové situaci zavádíme pojem doplněk množiny.
Je-li B \subseteq A, pak doplňkem množiny B vzhledem k množině A je množina, která obsahuje všechny prvky z A, které zároveň nejsou v B.
Doplněk množiny B vzhledem k množině A budeme značit B'_A. Pokud je z předchozího kontextu jasné, k jaké množině je doplněk vztažen, můžeme psát zkráceně B'.
Pozor, někdy se také doplněk značí \bar{B} . S tímto zápisem se setkáte zejména ve starší literatuře a v příkladech na konci tohoto textu.
Je asi také zřejmé, že operace doplňku není komutativní, neboli když zaměníme pozice množin A a B, nedostaneme stejný výsledek (nejen to, dokonce pak většinou není možné o doplňku mluvit, protože je porušena podmínka inkluze / podmnožiny). Graficky si můžeme doplněk znázornit následovně (doplněk je vyznačen šrafováním):
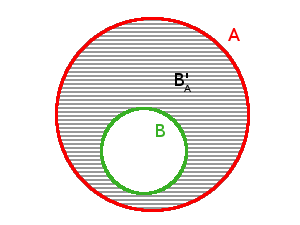
Řekli jsme si, že doplněk je také množina, zavedli jsme si tedy operaci, která nám umožňuje definovat novou množinu ze dvou již známých množin. Nesmíme však zapomenout na podmínku, že množina, jejíž určujeme doplněk, musí být podmnožinou množiny, vzhledem ke které se doplněk tvoří! Nyní si ukažme několik příkladů na konkrétních množinách:
- Budeme-li za A považovat množinu všech trojúhelníků v nějaké dané rovině a množina B bude množina všech ostroúhlých trojúhelníků tamtéž, pak množina B'_A bude množina všech tupoúhlých a pravoúhlých trojúhelníků v dané rovině – z množiny A totiž odebereme všechny prvky obsažené zároveň v její podmnožině B (tedy všechny ostroúhlé trojúhelníky).
- Mějme množiny A=\{1;2;3;4;5;6\}, B=\{1;3;6\}. Pak je množina B'_A=\{2;4;5\}.
- Jsou dány množiny C=\{x \in \N;x>5\}, D=\{6;7\}. Pak je množina D'_C=\{x \in \N; x>7\}.
- Říkali jsme si, že množina je sama sobě podmnožinou. Máme-li množinu M, pak M'_M = \varnothing .
Pokud použijeme obrazné vyjadřování, můžeme říci, že doplněk množiny B vzhledem k množině A je právě ten „zbytek“ množiny A, který zbyde po „odstřižení“ její podmnožiny B.
Rozdíl množin
U doplňku množin jsme byli velmi omezeni podmínkou, kdy jedna množina musela být podmnožinou druhé. Nyní si ukážeme operaci, která je doplňku podobná, avšak toto omezení nemá. Rozdíl množin totiž „ukousne“ z jedné množiny to, co má společné s množinou druhou. Rozdíl množin A a B budeme značit A-B a jeho definice je:
Rozdíl množin A a B, který značíme A-B, je množina, která obsahuje všechny prvky množiny A s výjimkou těch, jež jsou zároveň prvky množiny B.
Což můžeme říci také jinak: Chceme-li vytvořit množinu A-B, pak stačí vzít množinu A a vyjmout z ní prvky, které má společné s množinou B. I zde je zřejmé, že ani rozdíl není komutativní. Grafické znázornění rozdílu může vypadat např. takto:
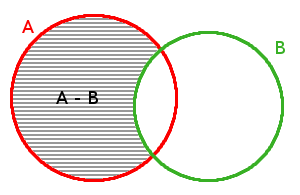
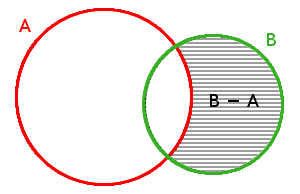
Můžeme se setkat také s odlišným značením rozdílu, přičemž platí, že následující dva zpisy jsou totožné.
A-B \iff A \setminus B
I rozdíl množin si samozřejmě ukážeme na konkrétních příkladech, měli bychom také poukázat na některé speciální případy:
- Mějme množiny A=\{1;2;3;4;5;6\}, B=\{1;3;6;8\}. Pak je množina A \setminus B=\{2; 4; 5\}.
- Jsou-li množiny C=\N a D=\{x \in \N; x>5\}. Pak je množina C-D=\{1;2;3;4;5\}.
- Zkusíme-li provést rozdíl množiny se sebou, získáme prázdnou množinu: M-M=\varnothing.
- Jak dopadne rozdíl u dvou množin, které nemají žádné společné prvky? Výsledkem bude původní množina, od které „odečítáme“, protože z ní podle definice rozdílu odebereme všechny prvky, které jsou současně v druhé množině, a těch je nula. Tedy např. bude-li A=\N a B=\{0;-1;-2;-3\}. Pak A-B=A=\N.
- Pokud nastane situace, kdy jedna množina je podmnožinou druhé, mohou nastat dva případy podle toho, jaké pořadí množin zvolíme v rozdílu. Budeme mít dvě množiny C, D, pro něž platí C \subseteq D. Pak C-D=\varnothing, protože z C odebereme všechny její prvky (všechny totiž patří i do množiny D). Opačný rozdíl je také zajímavý: D-C=C'_D. V tomto speciálním případě se tedy rozdíl chová stejně jako doplněk (z množiny D totiž odebereme všechny její prvky, které jsou zároveň prvky množiny C).
- Pro libovolnou množinu M také platí: M \setminus \varnothing = M. Prázdná množina neobsahuje žádné prvky, proto nemůže mít žádné prvky společné s množinou M, a tak výsledkem takového rozdílu musí být opět množina M.
Obrazně opět můžeme hovořit o „odstřihnutí“ části množiny, a to konkrétně té části, kterou má společnou s množinou, jíž „odečítáme“.
Příklady k procvičení: vypočtěte příklady 24.10 (rozdíly množin), 24.11 (ve výsledkách je špatně vidět kdy je množina doplňkem. Pozor, dívejte se pozorně na pruh nad písmenkem!), v těchto příkladech využívejte primárně průnik, sjednocení a rozdíl. Doplněk využívejte zcela minimálně (složité zbytečně). Výsledky jsou orientační a jsou přes doplňky, nicméně každý příklad má více správného řešení a výsledky můžou být matoucí. 24.25 a), b)
KRIEGELSTEIN, Eduard. Sbírka úloh z matematiky pro střední průmyslové školy a střední zemědělské technické školy. 10. vyd. Praha: Státní pedagogické nakladatelství, 1965.